本文解析PyTorch Geometric中异构GNNs的消息传递机制,利用计算图解释了如何处理不同节点类型的特征信息,深入理解图神经网络的工作原理。
原文标题:从节点到知识:PyTorch Geometric的异构消息传递解析
原文作者:数据派THU
冷月清谈:
核心内容是消息传递机制的解析,包括聚合器A、投影器B和聚合器C三个关键组件。聚合器A负责聚合相同源节点类型的信息;投影器B对不同源节点类型的特征向量进行线性投影以统一维度;聚合器C则聚合相同目标节点类型的信息。文章通过同构和异构网络的计算图示例,逐步演示了消息传递过程,并解释了每个组件的作用。
最后,文章展示了一个更复杂的异构网络示例,其中多个节点连接到目标节点,并解释了如何在计算图中聚合异构节点的特征信息。通过理解消息在不同数据集的计算图中的处理方式,可以更深入地了解图神经网络的工作原理,并利用异构图GNNs揭示复杂信息中的模式和洞察。
怜星夜思:
2、在实际应用中,如何确定一个图是否是异构图?除了文章中提到的特征维度不同之外,还有哪些判断依据?
3、文章主要关注消息传递机制。除了消息传递,异构图神经网络还有什么其他的关键技术?
原文内容
来源:DeepHub IMBA本文约2600字,建议阅读8分钟
本文将深入探讨异构GNNs,它们可以处理不同的节点类型及其独特特征。
图神经网络(GNNs)是预测复杂系统行为的强大工具:例如社交网络、金融交易,或作者、论文和学术场所之间的联系。虽然许多GNN教程专注于具有单一节点类型的简单图,但现实世界的系统通常更加复杂,需要异构图。
本文将深入探讨异构GNNs,它们可以处理不同的节点类型及其独特特征。我们将使用PyTorch Geometric的heteroconv层作为构建块。我们将详细解释任何异构数据集中的消息如何在计算图中处理。这将使你能够开始使用异构图神经网络。
图
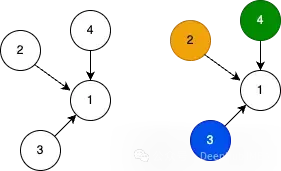
下面展示了两种图:具有相同节点类型的同构图和具有不同节点类型连接的异构图。但是什么使一个节点类型与另一个节点类型不同?答案很简单:特征!这里左边是一个同构网络,右边是一个异构网络:
对于同构图,节点1、2、3和4的所有特征具有相同的解释。例如,它们都有两个特征,x和z,我可以在节点之间进行比较。网络内的边只连接相同类型的节点。对于异构图,我们也描绘了节点1、2、3和4,具有类似的连接,但在这种情况下,每个节点类型都是唯一的,如颜色所示。
这意味着节点1的特征与节点2、3和4的特征不兼容。最简单的例子是,当节点1的特征维度与节点2、3和4不同。
许多现实世界的系统都是异构的。例如,作者合著论文,这些论文在会议上发表。对于作者节点,可能存储姓名和大学隶属关系等信息;对于论文,存储标题和摘要;对于会议,存储名称和地址和相关信息。当一组作者合著一篇在特定会议上发表的论文时,就会存在链接。但是相同节点类型的特征是可比较的,而不同节点类型的特征是不可比较的。
所以我们首先要知道如何存储同构网络信息和异构网络信息。
数据
我们生成合成数据来演示MessagePassing如何处理异构数据结构。
同构数据
我们为上面描述的网络生成一些合成数据。对于同构网络,有四个节点和单一节点类型;因此所有节点的特征具有相同的维度。我们将数据存储在单个张量中,如下所示:
x = torch.tensor([[0.1234, 0.2345], [0.2303, -0.1863], [-1.1229, -0.6380], [2.2082, 0.7080]])
边索引,描述连接的文件,定义如下:
edge_index = torch.tensor([[1, 2, 3], [0, 0, 0]])
这里我们只包括指向节点1(索引0)的边。
异构数据
在异构数据定义中,我们每种数据类型都有不同的维度。创建不同的特征集,即不同的特征维度。在示例图中有四种唯一类型:
-
A(节点1):特征维度2
-
B(节点2):特征维度3
-
C(节点3):特征维度4
-
D(节点4):特征维度5
因为每个节点类型具有不同的维度,我们必须将它们存储在单独的张量中。以下是节点1、2、3和4的节点特征:
节点1特征,维度2:
x_1 = torch.tensor([[0.1234, 0.2345]])
节点2特征,维度3:
x_2 = torch.tensor([[0.2303, -0.1863, 0.5213]])
节点3特征,维度4:
x_3 = torch.tensor([[-1.1229, -0.6380, 0.8640, 0.1297]])
节点4特征,维度5:
x_4 = torch.tensor([[2.2082, 0.7080, -0.9620, 0.1297, 0.3769]])
接下来是MessagePassing算法。
消息传递
卷积层是MessagePassing算法的扩展。我们这里只讨论一个重要的部分 - 计算图 - 而不深入过多细节。这个计算图与我们研究的网络不同!消息从源节点发送到目标节点,但在最终聚合的消息到达目标节点之前会发生多次转换。下图中展示了一个示意图。
计算图的示意表示
以下是每个转换框的高级概述:
-
聚合器A : 聚合相同源节点类型的信息。可用的聚合选项有 "sum" "mean", "min", "max" 或 "mul"
-
投影器B (SAGEConv层) :统一各种源节点类型维度的线性投影。
-
聚合器C : 聚合相同目标节点类型的信息。可用的聚合选项有 "sum", "mean", "min", "max", "cat", [None],默认为 "sum"。
聚合器A是MessagePassing算法的一部分;消息根据所选的聚合方案进行聚合。
投影器B是SAGEConv层的一部分;要使用异构层,必须使用支持OptPairTensor类型的conv层。或者说它必须能够接受不同的源和目标节点类型。其他支持这一点的PYG层有GATConv和PPFConv。
聚合器C是HeteroConv层的一部分;A的所有聚合消息都被收集并组合成每个节点类型的一个特征向量。
同构网络的计算图
在第一个例子中,我们创建了一个具有同构数据的数据集:
同构网络(左)的计算图(右),其中信息从源节点传播到目标节点1。
这个计算图更新节点1的值。节点2、3和4的消息被发送到节点1。因为源节点具有相同的类型,聚合器A通过取平均值来聚合所有特征。
-
0.4399 = (0.2345 — 1.1229 + 2.2082) / 3
-
-0.1980 = (0.2303–0.1863–0.6380) / 3
投影层B将特征向量[0.4399, -0.1980]通过线性层转换为一维向量0.6743。这里的一维是任意的,这可以是设置的任何维度。另外SAGEConv实现OptPairTensor的方式可能与其他层不同。
聚合器C在HeteroConv层中收集所有发送到节点1的消息,不考虑类型。所以最终得到了只有一种类型。聚合器C将原始消息0.6743传递给节点1。
异构网络的计算图
在第二个数据示例中,我们以使每个节点类型唯一的方式存储相同的数据。
异构网络(左)的计算图(右),其中信息从源节点传播到目标节点1。
有三个聚合器A,因为有三种不同的节点类型 - 节点2、3和4是唯一的!聚合器A取单个消息的平均值并将其传递给线性投影器B。
有三个线性投影器,每种节点类型一个。线性投影器B的工作方式与之前类似;它将2维向量投影到一维向量。
聚合器C收集所有以节点1为目标的消息。收到三条消息,每种唯一源节点类型一条消息。聚合器C对传入消息的值求和,并将其传递给节点1。
可以看到相同的数据却得到了完全不同的结果!
在最后一个数据集中,我们为每种节点类型添加多个节点,并将它们连接到节点1。这样就得到一个计算图,其中多个节点在被发送到线性投影层之前由聚合器A聚合。下图显示了这个数据集的计算图:
异构网络(左)的计算图(右),其中信息从源节点传播到目标节点1。在计算图中只显示了每种节点类型的第一个特征。
可以看到聚合器A聚合了相同节点类型的特征信息。但本质上我们有3个同构数据集和聚合器。在投影层之后,特征再次成为由C聚合的同构数据集。这种计算图设计使我们能够在图中聚合异构节点的特征信息。
总结
以上就是关于异构图神经网络的消息传递的完整流程。通过理解消息如何在不同数据集的计算图中处理,我们可以更深入的了解图神经网络的工作原理。将这些概念应用到数据中,可以发现异构图神经网络在揭示复杂、相互连接信息中有价值的洞察和模式方面的强大力量。