TimeDART通过自监督学习和扩散模型相结合,提供了一种新方法来提升时间序列预测的准确性。
原文标题:TimeDART:基于扩散自回归Transformer 的自监督时间序列预测方法
原文作者:数据派THU
冷月清谈:
怜星夜思:
2、扩散自回归模型相比传统模型有什么优势?
3、有哪些实际场景可以应用TimeDART的预测模型?
原文内容
来源:DeepHub IMBA本文约4000字,建议阅读5分钟本文介绍了基于扩散自回归Transformer 的自监督时间序列预测方法。
近年来,随着机器学习技术的进步,深度神经网络已经成为解决时间序列预测问题的主流方法。这反映了学术界和工业界在利用先进技术处理序列数据复杂性方面的持续努力。
自监督学习概述
基本定义
在时间序列领域的应用
-
从未标记数据中学习通用表示
-
同时捕获数据中的长期依赖关系和局部细节特征
现有方法的问题
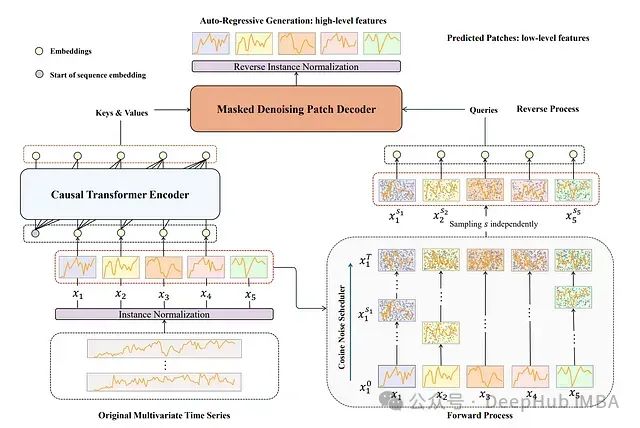
TimeDarT方法详解
核心技术组件
-
Transformer编码器设计:
-
使用了具有自注意力机制的Transformer编码器
-
专注于理解patches之间的依赖关系
-
有效捕获数据的整体序列结构
-
扩散和去噪过程:
-
实现了两个关键过程:扩散和去噪
-
通过向数据添加和移除噪声来捕获局部特征
-
这是所有扩散模型中的典型过程
-
提升了模型在详细模式上的表现
TimeDART架构详解
-
使用自回归生成捕获全局依赖关系
-
通过去噪扩散模型处理局部结构
-
在前向扩散过程中向输入patches引入噪声
-
生成自监督信号
-
通过自回归方式在反向过程中恢复原始序列
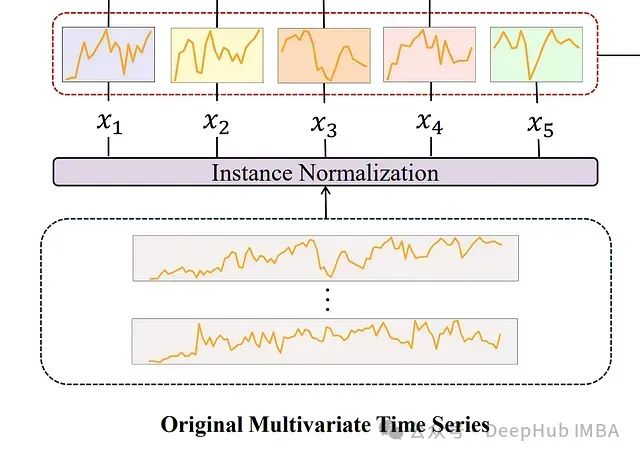
实例归一化和Patch嵌入
-
实例归一化:
-
对输入的多变量时间序列数据进行标准化
-
确保每个实例具有零均值和单位标准差
-
目的是保持最终预测的一致性
-
数据分割策略:
-
将时间序列数据划分为patches而非单个点
-
这种方法能够捕获更全面的局部信息
-
避免信息泄漏:
-
patch长度设置为等于stride(步长)
-
确保每个patch包含原始序列的非重叠段
-
防止训练过程中的信息泄漏
Transformer编码器中的Patch间依赖关系
-
基于自注意力的处理:
-
使用自注意力的Transformer编码器
-
专门用于建模patches之间的依赖关系
-
全局依赖性捕获:
-
通过考虑时间序列数据中不同patches之间的关系
-
有效捕获全局序列依赖关系
-
表示学习:
-
Transformer编码器能够学习有意义的patch间表示
-
这对于理解时间序列的高层结构至关重要
class TransformerEncoderBlock(nn.Module): def __init__( self, d_model: int, num_heads: int, feedforward_dim: int, dropout: float ): super(TransformerEncoderBlock, self).__init__()self.attention = nn.MultiheadAttention(
embed_dim=d_model, num_heads=num_heads, dropout=dropout, batch_first=True
)
self.norm1 = nn.LayerNorm(d_model)
self.ff = nn.Sequential(
nn.Linear(d_model, feedforward_dim),
nn.GELU(),
nn.Dropout(dropout),
nn.Linear(feedforward_dim, d_model),
)
self.conv1 = nn.Conv1d(in_channels=d_model, out_channels=feedforward_dim, kernel_size=1)
self.activation = nn.GELU()
self.conv2 = nn.Conv1d(in_channels=feedforward_dim, out_channels=d_model, kernel_size=1)
self.norm2 = nn.LayerNorm(d_model)
self.dropout = nn.Dropout(dropout)def forward(self, x, mask):
“”"
:param x: [batch_size * num_features, seq_len, d_model]
:param mask: [1, 1, seq_len, seq_len]
:return: [batch_size * num_features, seq_len, d_model]
“”"Self-attention
attn_output, _ = self.attention(x, x, x, attn_mask=mask)
x = self.norm1(x + self.dropout(attn_output))Feed-forward network
y = self.dropout(self.activation(self.conv1(y.permute(0, 2, 1))))
ff_output = self.conv2(y).permute(0, 2, 1)
ff_output = self.ff(x)
output = self.norm2(x + self.dropout(ff_output))
return output
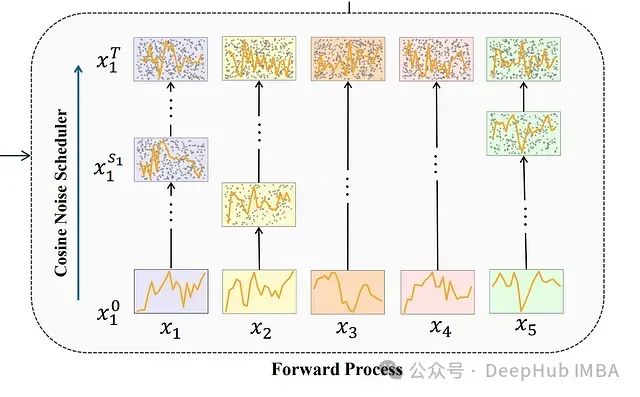
前向扩散过程
-
噪声应用:
-
在输入patches上应用噪声
-
生成自监督信号
-
通过从带噪声版本中重构原始数据来学习稳健的表示
-
模式识别:
-
噪声帮助模型识别和关注
-
专注于时间序列数据中的内在模式
class Diffusion(nn.Module):
def init(
self,
time_steps: int,
device: torch.device,
scheduler: str = “cosine”,
):
super(Diffusion, self).init()
self.device = device
self.time_steps = time_stepsif scheduler == “cosine”:
self.betas = self._cosine_beta_schedule().to(self.device)
elif scheduler == “linear”:
self.betas = self._linear_beta_schedule().to(self.device)
else:
raise ValueError(f"Invalid scheduler: {scheduler=}")self.alpha = 1 - self.betas
self.gamma = torch.cumprod(self.alpha, dim=0).to(self.device)def _cosine_beta_schedule(self, s=0.008):
steps = self.time_steps + 1
x = torch.linspace(0, self.time_steps, steps)
alphas_cumprod = (
torch.cos(((x / self.time_steps) + s) / (1 + s) * torch.pi * 0.5) ** 2
)
alphas_cumprod = alphas_cumprod / alphas_cumprod[0]
betas = 1 - (alphas_cumprod[1:] / alphas_cumprod[:-1])
return torch.clip(betas, 0, 0.999)def _linear_beta_schedule(self, beta_start=1e-4, beta_end=0.02):
betas = torch.linspace(beta_start, beta_end, self.time_steps)
return betasdef sample_time_steps(self, shape):
return torch.randint(0, self.time_steps, shape, device=self.device)def noise(self, x, t):
noise = torch.randn_like(x)
gamma_t = self.gamma[t].unsqueeze(-1) # [batch_size * num_features, seq_len, 1]x_t = sqrt(gamma_t) * x + sqrt(1 - gamma_t) * noise
noisy_x = torch.sqrt(gamma_t) * x + torch.sqrt(1 - gamma_t) * noise
return noisy_x, noisedef forward(self, x):
x: [batch_size * num_features, seq_len, patch_len]
t = self.sample_time_steps(x.shape[:2]) # [batch_size * num_features, seq_len]
noisy_x, noise = self.noise(x, t)
return noisy_x, noise, t
基于交叉注意力的去噪解码器
-
核心功能:
-
使用交叉注意力机制
-
目的是重构原始的、无噪声的patches
-
优化设计:
-
允许可调整的优化难度
-
使自监督任务更有效
-
使模型能够专注于捕获详细的patch内特征
-
接收噪声(作为查询)和编码器的输出(键和值)
-
使用掩码确保第j个噪声输入对应于Transformer编码器的第j个输出
class TransformerDecoderBlock(nn.Module): def __init__( self, d_model: int, num_heads: int, feedforward_dim: int, dropout: float ): super(TransformerDecoderBlock, self).__init__()self.self_attention = nn.MultiheadAttention(
embed_dim=d_model, num_heads=num_heads, dropout=dropout, batch_first=True
)
self.norm1 = nn.LayerNorm(d_model)
self.encoder_attention = nn.MultiheadAttention(
embed_dim=d_model, num_heads=num_heads, dropout=dropout, batch_first=True
)
self.norm2 = nn.LayerNorm(d_model)
self.ff = nn.Sequential(
nn.Linear(d_model, feedforward_dim),
nn.ReLU(),
nn.Dropout(dropout),
nn.Linear(feedforward_dim, d_model),
)
self.norm3 = nn.LayerNorm(d_model)
self.dropout = nn.Dropout(dropout)def forward(self, query, key, value, tgt_mask, src_mask):
“”"
:param query: [batch_size * num_features, seq_len, d_model]
:param key: [batch_size * num_features, seq_len, d_model]
:param value: [batch_size * num_features, seq_len, d_model]
:param mask: [1, 1, seq_len, seq_len]
:return: [batch_size * num_features, seq_len, d_model]
“”"Self-attention
attn_output, _ = self.self_attention(query, query, query, attn_mask=tgt_mask)
query = self.norm1(query + self.dropout(attn_output))Encoder attention
attn_output, _ = self.encoder_attention(query, key, value, attn_mask=src_mask)
query = self.norm2(query + self.dropout(attn_output))Feed-forward network
ff_output = self.ff(query)
x = self.norm3(query + self.dropout(ff_output))
return x
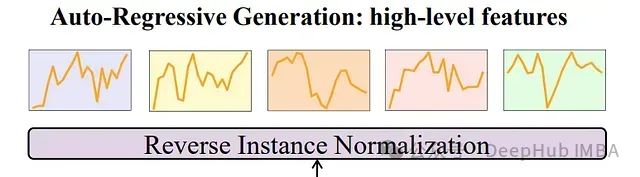
用于全局依赖关系的自回归生成
-
高层依赖捕获:
-
捕获时间序列中的高层全局依赖关系
-
通过自回归方式恢复原始序列
-
使模型能够理解整体时间模式和依赖关系
-
显著提升预测能力
class DenoisingPatchDecoder(nn.Module): def __init__( self, d_model: int, num_heads: int, num_layers: int, feedforward_dim: int, dropout: float, ): super(DenoisingPatchDecoder, self).__init__()self.layers = nn.ModuleList(
[
TransformerDecoderBlock(d_model, num_heads, feedforward_dim, dropout)
for _ in range(num_layers)
]
)
self.norm = nn.LayerNorm(d_model)def forward(self, query, key, value, is_tgt_mask=True, is_src_mask=True):
seq_len = query.size(1)
tgt_mask = (
generate_self_only_mask(seq_len).to(query.device) if is_tgt_mask else None
)
src_mask = (
generate_self_only_mask(seq_len).to(query.device) if is_src_mask else None
)
for layer in self.layers:
query = layer(query, key, value, tgt_mask, src_mask)
x = self.norm(query)
return xclass ForecastingHead(nn.Module):
def init(
self,
seq_len: int,
d_model: int,
pred_len: int,
dropout: float,
):
super(ForecastingHead, self).init()
self.pred_len = pred_len
self.flatten = nn.Flatten(start_dim=-2)
self.forecast_head = nn.Linear(seq_len * d_model, pred_len)
self.dropout = nn.Dropout(dropout)
def forward(self, x: torch.Tensor) -> torch.Tensor:
“”"
:param x: [batch_size, num_features, seq_len, d_model]
:return: [batch_size, pred_len, num_features]
“”"
x = self.flatten(x) # (batch_size, num_features, seq_len * d_model)
x = self.forecast_head(x) # (batch_size, num_features, pred_len)
x = self.dropout(x) # (batch_size, num_features, pred_len)
x = x.permute(0, 2, 1) # (batch_size, pred_len, num_features)
return x
优化和微调
-
自回归优化:
-
整个模型以自回归方式进行优化
-
获得可以针对特定预测任务进行微调的可迁移表示
-
表示特性:
-
确保模型学习的表示既全面又适应性强
-
能够适应各种下游应用
-
在时间序列预测中实现卓越性能
实验评估
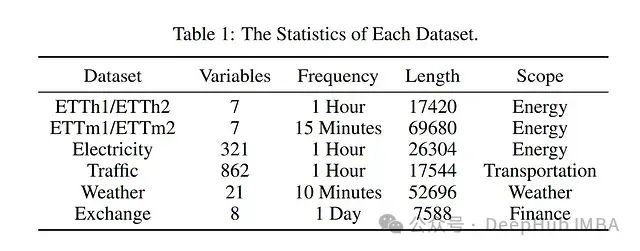
数据集介绍
-
ETT数据集系列:
-
ETTh1、ETTh2、ETTm1、ETTm2四个子集
-
代表能源领域的时间序列数据
-
其他领域数据集:
-
Weather数据集
-
Exchange数据集
-
Electricity数据集
-
Traffic数据集
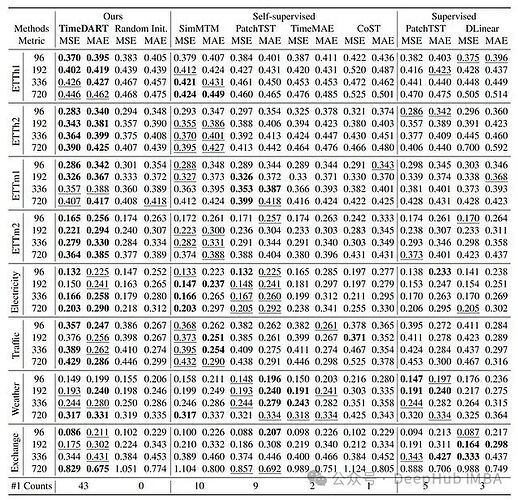
实验结果分析
-
与最先进的自监督方法和监督方法进行比较
-
最佳结果用粗体标示
-
第二好的结果带有下划线
-
"#1 Counts"表示该方法达到最佳结果的次数
-
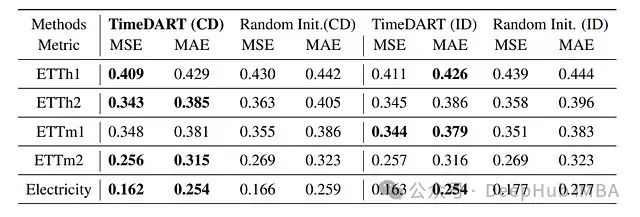
展示了在五个数据集上预训练并在特定数据集上微调的结果
-
所有结果都是从4个不同预测窗口{96, 192, 336, 720}中平均得出
-
最好的结果用粗体标示
-
所有结果都是从4个不同预测窗口{96, 192, 336, 720}中平均得出
-
最好的结果用粗体标示
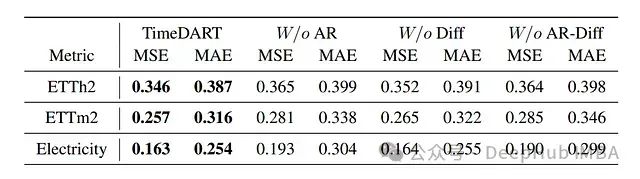
超参数敏感性分析
前向过程参数
-
噪声步数T的影响:
-
测试了{750, 1000, 1250}三个设置
-
发现噪声步数对预训练难度影响不大
-
所有设置都优于随机初始化
-
噪声调度器的选择:
-
余弦调度器显著优于线性调度器
-
某些情况下,线性调度器甚至导致性能低于随机初始化
-
证实了平滑噪声添加的重要性
去噪patch解码器层数
-
测试了{0, 1, 2, 3}层配置
-
单层解码器通常提供最佳的模型复杂度和准确性平衡
-
过多的层数可能导致表示网络的训练不足
patch长度的影响
-
测试了{1, 2, 4, 8, 16}不同长度
-
最佳patch长度取决于数据集特征
-
较大的patch长度可能更适合具有高冗余性的数据集
总结
-
技术创新:
-
首次将扩散和自回归建模统一到单一框架
-
设计了灵活的交叉注意力去噪网络
-
性能提升:
-
在多个数据集上实现了最优性能
-
展示了强大的域内和跨域泛化能力
-
实际意义:
-
为时间序列预测提供了新的研究方向
-
为实际应用提供了更可靠的预测工具