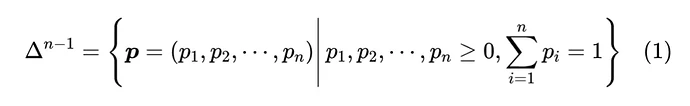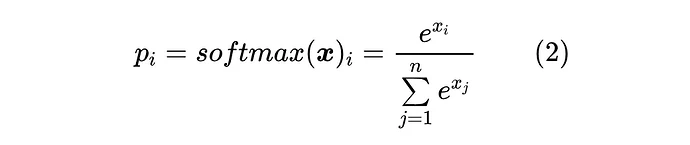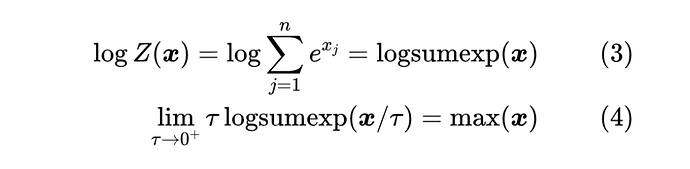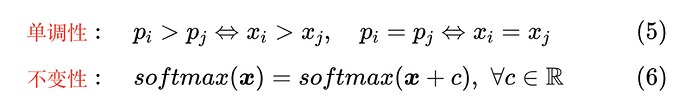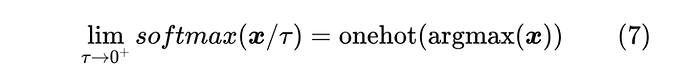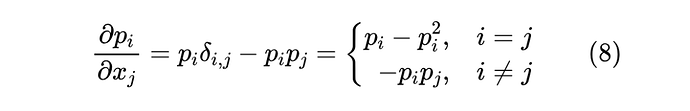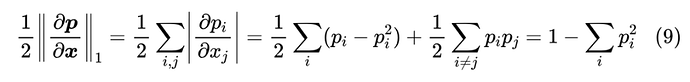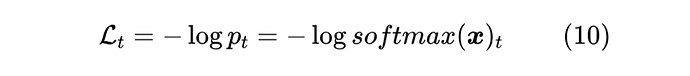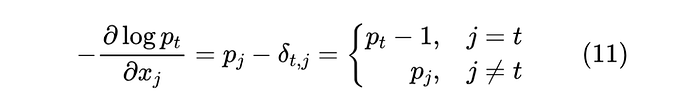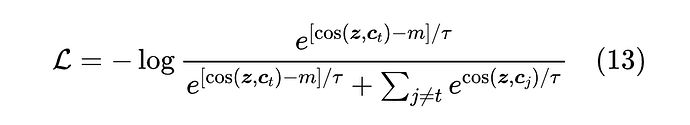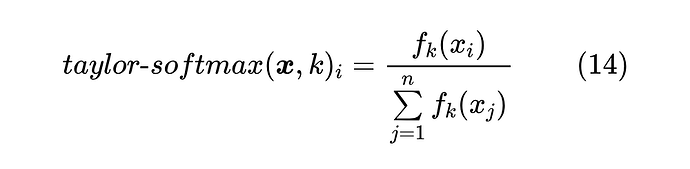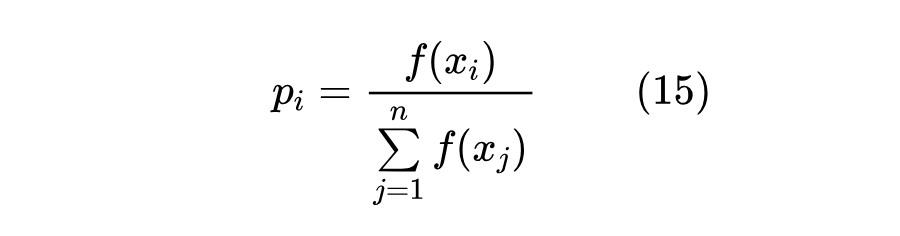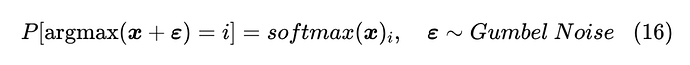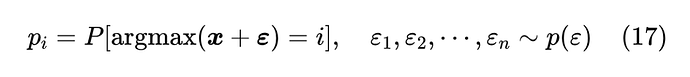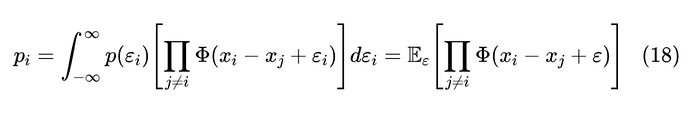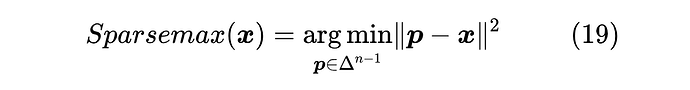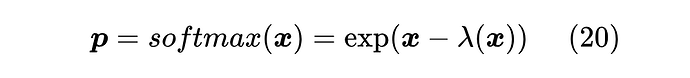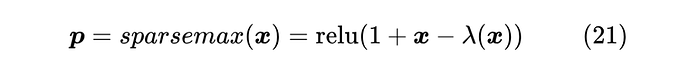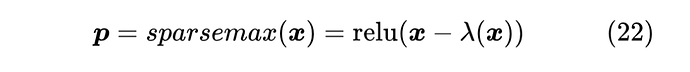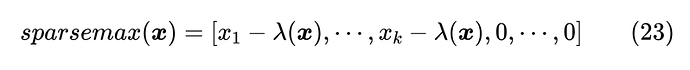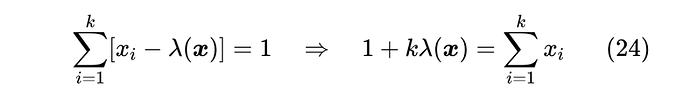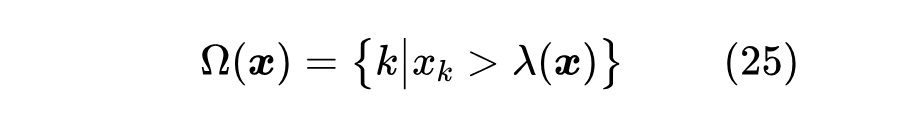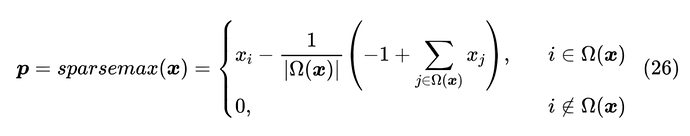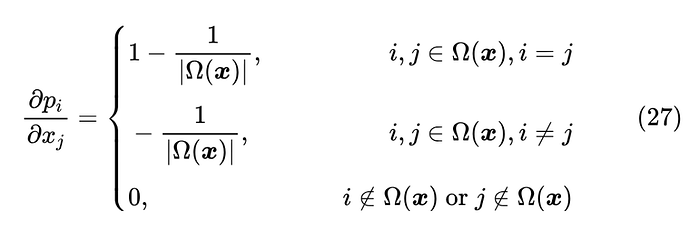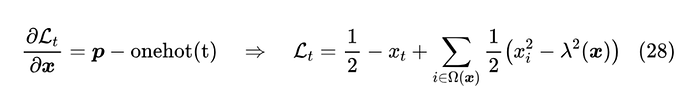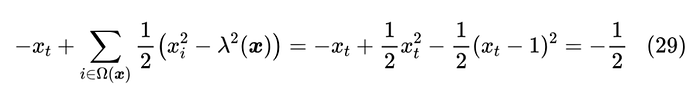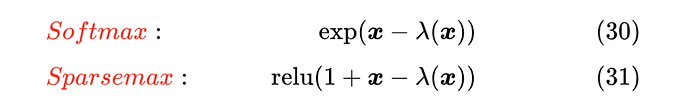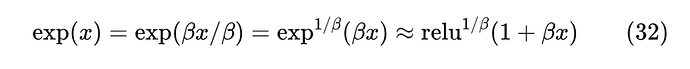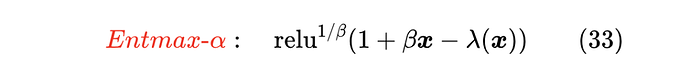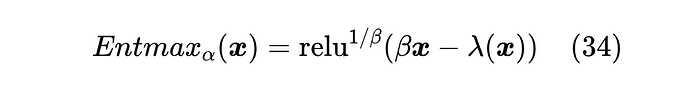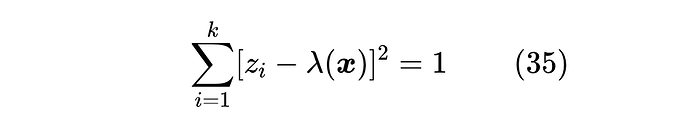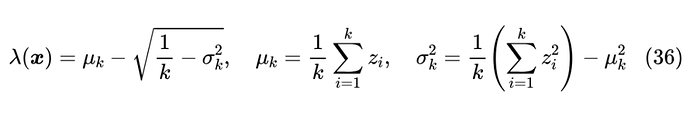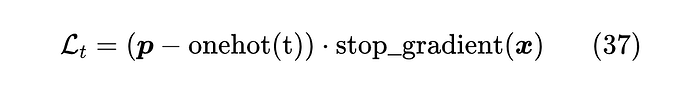本文总结了Softmax及其变体的性质与应用，探讨其在概率分布构建中的重要性与挑战。
原文标题：通向概率分布之路：盘点Softmax及其替代品
原文作者：数据派THU
冷月清谈：
本文回顾了Softmax的基本定义及其重要性质，如单调性和不变性，探讨了Softmax在深度学习中用于概率分布构建的重要性。文章详细对比了多种Softmax的变体，包括Margin Softmax、Taylor Softmax、Sparse Softmax等，分析了这些替代方案在特定场景下的优势和局限性。此外，讨论了如何通过不同损失函数优化模型性能，尤其是交叉熵损失的应用，以及如何应对在特定任务（如长尾分类和稀疏性）中Softmax表现不佳的问题。最后，文章提出了新型的概率分布构建方法Perturb Max，并呼应了大数据及深度学习领域的最新发展。
怜星夜思：
1、在何种场景下使用Softmax可能会导致模型过度自信？
2、Softmax与其他概率分布近似方法相比，有哪些优缺点？
3、在训练模型时，如何选择合适的损失函数？
2、Softmax与其他概率分布近似方法相比，有哪些优缺点？
3、在训练模型时，如何选择合适的损失函数？
原文内容
本文约7000字，建议阅读10分钟在这篇文章中，我们将简单总结一下 Softmax 的相关性质，并盘点和对比一下它的部分替代方案。
不论是在基础的分类任务中，还是如今无处不在的注意力机制中，概率分布的构建都是一个关键步骤。具体来说，就是将一个 维的任意向量，转换为一个 元的离散型概率分布。众所周知，这个问题的标准答案是 Softmax，它是指数归一化的形式，相对来说比较简单直观，同时也伴有很多优良性质，从而成为大部分场景下的“标配”。
尽管如此，Softmax 在某些场景下也有一些不如人意之处，比如不够稀疏、无法绝对等于零等，因此很多替代品也应运而生。在这篇文章中，我们将简单总结一下 Softmax 的相关性质，并盘点和对比一下它的部分替代方案。
01 Softmax回顾
首先引入一些通用记号： 是需要转为概率分布的 n 维向量，它的分量可正可负，也没有限定的上下界。 定义为全体 元离散概率分布的集合，即
之所以标注 而不是 ，是因为约束 定义了 维空间中的一个 维子平面，再加上 的约束， 的集合就只是该平面的一个子集，即实际维度只有 。
基于这些记号，本文的主题就可以简单表示为探讨 的映射，其中 我们习惯称之为 Logits 或者 Scores。
02 基本定义
Softmax 的定义很简单：
Softmax 的来源和诠释都太多了，比如能量模型、统计力学或者单纯作为 的光滑近似等，所以我们很难考证它的最早出处，也不去做这个尝试了。很多时候我们也会加上一个温度参数，即考虑 ，但 tau 本身也可以整合到 的定义之中，因此这里不特别分离出 参数。
Softmax 的分母我们通常记为 ，它的对数就是大多数深度学习框架都自带的 运算，他它是 的一个光滑近似：
当 取1时，就可以写出 ， 方差越大近似程度越高，更进一步的讨论可以参考《寻求一个光滑的最大值函数》[1]。
03 两点性质
除了将任意向量转换为概率分布外，Softmax 还满足两点性质
单调性意味着 Softmax 是保序的， 的最大值/最小值跟 的最大值/最小值相对应；不变性说的是 的每个分量都加上同一个常数，Softmax 的结果不变，这跟 的性质是一样的，即同样有 。
因此，根据这两点性质我们可以得出，Softmax实际是 一个光滑近似（更准确来说是 的光滑近似），更具体地我们有
这大概就是 Softmax 这个名字的来源。注意不要混淆了，Softmax 是 而不是 的光滑近似， 的光滑近似是 才对。
04 梯度计算
对于深度学习来说，了解一个函数的性质重要方式之一是了解它的梯度，对于 Softmax，我们在《从梯度最大化看Attention的Scale操作》曾经算过：
这样排列成的矩阵也称为 Softmax 的雅可比矩阵（Jacobian Matrix）[2]，它的 L1 范数有一个简单的形式
当 是 one hot 分布时，上式等于 0，这意味着 Softmax 的结果越接近 one hot，它的梯度消失现象越严重，所以至少初始化阶段，我们不能将 Softmax 初始化得接近 one hot。同时上式最右端也联系到了 Rényi 熵的概念，它跟常见的香侬熵类似。
05 参考实现
Softmax 的直接实现很简单，直接取 然后归一化就行，Numpy 的参考代码为：
def softmax(x):
y = np.exp(x)
return y / y.sum()
然而，如果 中存在较大的分量，那么算 时很容易溢出，因此我们通常都要利用 Softmax 的不变性，先将每个分量减去所有分量的最大值，然后再算 Softmax，这样每个取 的分量都不大于 0，确保不会溢出：
def softmax(x):
y = np.exp(x - x.max())
return y / y.sum()
06 损失函数
构建概率分布的主要用途之一是用于构建单标签多分类任务的输出，即假设有一个 分类任务， 是模型的输出，那么我们希望通过 来预测每个类的概率。为了训练这个模型，我们需要一个损失函数，假设目标类别是 ，常见的选择是交叉熵损失：
我们可以求得它的梯度：
注意 是给定的，所以 实际表达的是目标分布 ，而全体 就是 本身，所以上式可以更直观地写成：
也就是说，它的梯度正好是目标分布与预测分布之差，只要两者不相等，那么梯度就一直存在，优化就可以持续下去，这是交叉熵的优点。当然，某些情况下这也是缺点，因为 Softmax 只有在 才会得到 one hot，换言之正常情况下都不会出现 one hot，即优化一直不会完全停止，那么就有可能导致过度优化，这也是后面的一些替代品的动机。
除了交叉熵之外，还有其他一些损失可用，比如 ，这可以理解为准确率的光滑近似的相反数，但它可能会有梯度消失问题，所以它的优化效率往往不如交叉熵，一般只适用于微调而不是从零训练，更多讨论可以参考《如何训练你的准确率？》。
07 Softmax变体
介绍完 Softmax，我们紧接着总结一下本博客以往讨论过 Softmax 的相关变体工作，比如 Margin Softmax、Taylor Softmax、Sparse Softmax 等，它们都是在 Softmax 基础上的衍生品，侧重于不同方面的改进，比如损失函数、、稀疏性、长尾性等。
08 Margin Softmax
首先我们介绍起源于人脸识别的一系列 Softmax 变体，它们可以统称为 Margin Softmax，后来也被应用到 NLP 的 Sentence Embedding 训练之中，本站曾在《基于GRU和am-softmax的句子相似度模型》[3] 讨论过其中的一个变体 AM-Softmax，后来则在《从三角不等式到Margin Softmax》有过更一般的讨论。
尽管 Margin Softmax 被冠以 Softmax 之名，但它实际上更多是一种损失函数改进。以 AM-Softmax 为例，它有两个特点：第一，以 形式构造 Logits，即 的形式，此时的温度参数 是必须的，因为单纯的 值域为 ，不能拉开类概率之间的差异；第二，它并不是简单地以 为损失，而是做了加强：
直观来看，就是交叉熵希望 是 所有分量中最大的一个，而 AM-Softmax 则不仅希望 最大，还希望它至少比第二大的分量多出 ，这里的 就称为 Margin。
为什么要增加对目标类的要求呢？这是应用场景导致的。刚才说了，Margin Softmax 起源于人脸识别，放到 NLP 中则可以用于语义检索，也就是说它的应用场景是检索，但训练方式是分类。如果单纯用分类任务的交叉熵来训练模型，模型编码出来的特征不一定能很好地满足检索要求，所以要加上 Margin 使得特征更加紧凑一些。
09 Taylor Softmax
接下来要介绍的，是在《exp(x)在x=0处的偶次泰勒展开式总是正的》讨论过的 Taylor Softmax，它利用了 的泰勒展开式的一个有趣性质：
对于任意实数 及偶数 ，总有 ，即 在 处的偶次泰勒展开式总是正的。
利用这个恒正性，我们可以构建一个 Softmax 变体（ 是任意偶数）：
由于是基于 的泰勒展开式构建的，所以在一定范围内 Taylor Softmax 与 Softmax 有一定的近似关于，某些场景下可以用 Taylor Softmax 替换 Softmax。那么 Taylor Softmax 有什么特点呢？答案是更加长尾，因为 Taylor Softmax 是多项式函数归一化，相比指数函数衰减得更慢，所以对于尾部的类别，Taylor Softmax 往往能够给其分配更高的概率，可能有助于缓解 Softmax 的过度自信现象。
Taylor Softmax 的最新应用，是用来替换 Attention 中的 Softmax，使得原本的平方复杂度降低为线性复杂度，相关理论推导可以参考《Transformer升级之路：作为无限维的线性Attention》[4]。
该思路的最新实践是一个名为 Based 的模型，它利用 来线性化 Attention，声称比 Attention 高效且比 Mamba 效果更好，详细介绍可以参考博客《Zoology（Blogpost 2）: Simple, Input-Dependent, and Sub-Quadratic Sequence Mixers》[5] 和《BASED: Simple linear attention language models balance the recall-throughput tradeoff》[6]。
10 Sparse Softmax
Sparse Softmax 是笔者参加 2020 年法研杯时提出的一个简单的 Softmax 稀疏变体，首先发表在《SPACES：“抽取-生成”式长文本摘要（法研杯总结）》，后来也补充了相关实验，写了篇简单的论文《Sparse-softmax: A Simpler and Faster Alternative Softmax Transformation》[7]。
我们知道，在文本生成中，我们常用确定性的 Beam Search 解码，或者随机性的 TopK/TopP Sampling 采样，这些算法的特点都是只保留了预测概率最大的若干个 Token 进行遍历或者采样，也就等价于将剩余的 Token 概率视为零，而训练时如果直接使用 Softmax 来构建概率分布的话，那么就不存在绝对等于零的可能，这就让训练和预测出现了不一致性。Sparse Softmax 就是希望能处理这种不一致性，思路很简单，就是在训练的时候也把 Top- 以外的 Token 概率置零：
其中 是将 从大到小排列后前 个元素的原始下标集合。简单来说，就是在训练阶段就进行与预测阶段一致的阶段操作。这里的 选取方式也可以按照 Nucleus Sampling 的 Top- 方式来操作，看具体需求而定。但要注意的是，Sparse Softmax 强行截断了剩余部分的概率，意味着这部分 Logits 无法进行反向传播了，因此 Sparse Softmax 的训练效率是不如 Softmax 的，所以它一般只适用于微调场景，而不适用于从零训练。
11 Perturb Max
这一节我们介绍一种新的构建概率分布的方式，这里称之为 Perturb Max，它是 Gumbel Max 的一般化，首次介绍于《从重参数的角度看离散概率分布的构建》，此外在论文《EXACT: How to Train Your Accuracy》[8] 也有过相关讨论，至于更早的出处笔者则没有进一步考究了。
12 问题反思
首先我们知道，构建一个 的映射并不是难事，只要 是 （实数到非负实数）的映射，如 ，那么只需要让
就是满足条件的映射了。如果要加上“两点性质” [9] 中的“单调性”呢？那么也不难，只需要保证 的单调递增函数，这样的函数也有很多，比如 。但如果再加上“不变性”呢？我们还能随便写出一个满足不变性的 映射吗？（反正我不能）
可能有读者疑问：为什么非要保持单调性和不变性呢？的确，单纯从拟合概率分布的角度来看，这两点似乎都没什么必要，反正都是“力大砖飞”，只要模型足够大，那么没啥不能拟合的。但从 “Softmax 替代品”这个角度来看，我们希望新定义的概率分布同样能作为 的光滑近似，那么就要尽可能多保持跟 相同的性质，这是我们希望保持单调性和不变性的主要原因。
13 Gumbel Max
Perturb Max 借助于Gumbel Max 的一般化来构造这样的一类分布。不熟悉 Gumbel Max 的读者，可以先到《漫谈重参数：从正态分布到Gumbel Softmax》[10] 了解一下 Gumbel Max。简单来说，Gumbel Max 就是发现：
怎么理解这个结果呢？首先，这里的 是指 的每个分量都是从 Gumbel 分布独立 [11] 重复采样出来的；接着，我们知道给定向量 ，本来 是确定的结果，但加了随机噪声 之后， 的结果也带有随机性了，于是每个 都有自己的概率；最后，Gumbel Max 告诉我们，如果加的是 Gumbel 噪声，那么i的出现概率正好是 。
Gumbel Max 最直接的作用，就是提供了一种从分布 中采样的方式，当然如果单纯采样还有更简单的方法，没必要“杀鸡用牛刀”。Gumbel Max 最大的价值是“重参数（Reparameterization）”，它将问题的随机性从带参数 的离散分布转移到了不带参数的 上，再结合 Softmax 是 的光滑近似，我们得到 是 Gumbel Max 的光滑近似，这便是 Gumbel Softmax，是训练“离散采样模块中带有可学参数”的模型的常用技巧。
14 一般噪声
Perturb Max 直接源自 Gumbel Max：既然 Softmax 可以从 Gumbel 分布中导出，那么如果将 Gumbel 分布换为一般的分布，比如正态分布，不就可以导出新的概率分布形式了？也就是说直接定义
重复 Gumbel Max 的推导，我们可以得到
其中 是 的累积概率函数。对于一般的分布，哪怕是简单的标准正态分布，上式都很难得出解析解，所以只能数值估计。为了得到确定性的计算结果，我们可以用逆累积概率函数的方式进行均匀采样，即先从 均匀选取 ，然后通过求解 来得到 。
从 Perturb Max 的定义或者最后 的形式我们都可以断言 Perturb Max 满足单调性和不变性，这里就不详细展开了。那它在什么场景下有独特作用呢？说实话，还真不知道，《EXACT: How to Train Your Accuracy》[8] 一文用它来构建新的概率分布并优化准确率的光滑近似，但笔者自己的实验显示没有特别的效果。个人感觉，可能在某些需要重参数的场景能够表现出特殊的作用吧。
15 Sparsemax
接下来要登场的是名为 Sparsemax 的概率映射，出自 2016 年的论文《From Softmax to Sparsemax: A Sparse Model of Attention and Multi-Label Classification》[12]，它跟笔者提出的 Sparse Softmax 一样，都是面向稀疏性的改动，但作者的动机是用在 Attention 中提供更好的可解释性。跟 Sparse Softmax 直接强行截断 Top- 个分量不同，Sparsemax 提供了一个更为自适应的稀疏型概率分布构造方式。
16 基本定义
原论文将 Sparsemax 定义为如下优化问题的解：
通过拉格朗日乘数法就可以求出精确解的表达式。然而，这种方式并不直观，而且也不容易揭示它跟 Softmax 的联系。下面提供笔者构思的一种私以为更加简明的引出方式。
首先，我们可以发现，Softmax 可以等价地表示为
其中 是使得 的各分量之和为 1 的常数，对于 Softmax 我们可以求出 。
然后，在 Taylor Softmax 那一节我们说了， 的偶次泰勒展开总是正的，因此可以用偶次泰勒展开来构建 Softmax 变体。但如果是奇数次呢？比如 ，它并不总是非负的，但我们可以加个 强行让它变成非负的，即 ，用这个近似替换掉式（20）的 ，就得到了 Sparsemax：
其中 依然是使得 的各分量之和为1的常数，并且常数 1 也可以整合到 之中，所以上式也等价于
17 求解算法
到目前为止，Sparsemax 还只是一个形式化的定义，因为 的具体计算方法尚不清楚，这就是本节需要探讨的问题。不过即便如此，单靠这个定义我们也不难看出 Sparsemax 满足单调性和不变性两点性质，如果还觉得不大肯定的读者，可以自行尝试证明一下它。
现在我们转向 的计算。不失一般性，我们假设 各分量已经从大到小排序好，即 ，接着我们不妨先假设已知 ，那么很显然
根据 的定义，我们有
这就可以求出 。当然，我们无法事先知道 ，但我们可以遍历 ，利用上式求一遍 ，取满足 ，这也可以等价地表示为求满足 的最大的 ，然后返回对应的
参考实现：
def sparsemax(x):
x_sort = np.sort(x)[::-1]
x_lamb = (np.cumsum(x_sort) - 1) / np.arange(1, len(x) + 1)
lamb = x_lamb[(x_sort >= x_lamb).argmin() - 1]
return np.maximum(x - lamb, 0)
18 梯度计算
方便起见，我们引入记号
那么可以写出
从这个等价形式可以看出，跟 Sparse Softmax 一样，Sparsemax 同样也只对部分类别有梯度，可以直接算出雅可比矩阵：
由此可以看出，对于在 里边的类别，Sparsemax 倒是不会梯度消失，因为此时它的梯度恒为常数，但它总的梯度大小，取决于 的元素个数，它越少则越稀疏，意味着梯度也越稀疏。
19 损失函数
最后我们来讨论 Sparsemax 作为分类输出时的损失函数。比较直观的想法就是跟 Softmax 一样用交叉熵 ，但 Sparsemax 的输出可能是严格等于0的，所以为了防止 错误，还要给每个分量都加上 ，最终的交叉熵形式为 ，但这一来有点丑，二来它还不是凸函数，所以并不是一个理想选择。
事实上，交叉熵在 Softmax 中之所以好用，是因为它的梯度恰好有（12）的形式，所以对于 Sparsemax，我们不妨同样假设损失函数的梯度为 ，然后反推出损失函数该有的样子，即：
从右往左验证比较简单，从左往右推可能会有些困难，但不多，反复拼凑一下应该就能出来了。第一个 常数是为了保证损失函数的非负性，我们可以取一个极端来验证一下：假设优化到完美，那么 应该也是 one hot，此时 ，并且 ，于是
所以要多加上常数 。
20 Entmax-α
Entmax- 是 Sparsemax 的一般化，它的动机是 Sparsemax 往往会过度稀疏，这可能会导致学习效率偏低，导致最终效果下降的问题，所以 Entmax- 引入了 参数，提供了 Softmax（ ）到Sparsemax（ ）的平滑过度。
Entmax- 出自论文《Sparse Sequence-to-Sequence Models》[13]，作者跟 Sparsemax 一样是 Andre F. T. Martins，这位大佬围绕着稀疏 Softmax、稀疏 Attention 做了不少工作，有兴趣的读者可以在他的主页 [14] 查阅相关工作。
21 基本定义
跟 Sparsemax 一样，原论文将 Entmax- 定义为类似（19）的优化问题的解，但这个定义涉及到 Tsallis entropy [15] 的概念（也是 Entmax 的 Ent 的来源），求解还需要用到拉格朗日乘数法，相对来说比较复杂，这里不采用这种引入方式。
我们的介绍同样是基于上一节的近似 ，对于 Softmax 和 Sparsemax，我们有
Sparsemax 太稀疏，背后的原因也可以理解为 近似精度不够高，我们可以从中演化出更高精度的近似
只要 ，那么最右端就是一个比 更好的近似（想想为什么）。利用这个新近似，我们就可以构建
这里 是为了对齐原论文的表达方式，事实上用 表示更简洁一些。同样地，常数 1 也可以收入到 定义之中，所以最终定义可以简化为
22 求解算法
对于一般的 ，求解 是比较麻烦的事情，通常只能用二分法求解。
首先我们记 ，并且不失一般性假设 ，然后我们可以发现 Entmax- 是满足单调性和不变性的，借助不变性我们可以不失一般性地设 （如果不是，每个 都减去 即可）。
现在可以检验，当 时， 的所有分量之和大于等于 1，当 时， 的所有分量之和等于 0，所以最终能使分量之和等于 1 的 必然在 内，然后我们就可以使用二分法来逐步逼近最优的 。
对于某些特殊的 ，我们可以得到一个求精确解的算法。Sparsemax 对应 ，我们前面已经给出了求解过程，另外一个能给解析解的例子是 ，这也是原论文主要关心的例子，如果不加标注，那么 Entmax 默认就是 Entmax-1.5。跟 Sparsemax 一样的思路，我们先假设已知 ，于是有
这只不过是关于 的一元二次方程，可以解得
当我们无法事先知道 时，可以遍历 ，利用上式求一遍 ，取满足 那一个 ，但注意这时候不等价于求满足 的最大的 。
完整的参考实现：
def entmat(x):
x_sort = np.sort(x / 2)[::-1]
k = np.arange(1, len(x) + 1)
x_mu = np.cumsum(x_sort) / k
x_sigma2 = np.cumsum(x_sort**2) / k - x_mu**2
x_lamb = x_mu - np.sqrt(np.maximum(1. / k - x_sigma2, 0))
x_sort_shift = np.pad(x_sort[1:], (0, 1), constant_values=-np.inf)
lamb = x_lamb[(x_sort > x_lamb) & (x_lamb > x_sort_shift)]
return np.maximum(x / 2 - lamb, 0)**2
23 其他内容
Entmax- 的梯度跟 Sparsemax 大同小异，这里就不展开讨论了，读者自行推导一下或者参考原论文就行。至于损失函数，同样从梯度 出发反推出损失函数也是可以的，但其形式有点复杂，有兴趣了解的读者可以参考原论文《Sparse Sequence-to-Sequence Models》[13] 以及《Learning with Fenchel-Young Losses》[16]。
不过就笔者看来，直接用 算子来定义损失函数更为简单通用，可以避免求原函数的复杂过程：
这里的 是向量内积，这样定义出来的损失，其梯度正好是 ，但要注意这个损失函数只有梯度是有效的，它本身的数值是没有参考意义的，比如它可正可负，也不一定越小越好，所以要评估训练进度和效果的话，得另外建立指标（比如交叉熵或者准确率）。
24 文章小结
本文简单回顾和整理了 Softmax 及其部分替代品，其中包含的工作有 Softmax、Margin Softmax、Taylor Softmax、Sparse Softmax、Perturb Max、Sparsemax、Entmax- 的定义、性质等内容。
参考文献
[1] https://kexue.fm/archives/3290
[2] https://en.wikipedia.org/wiki/Jacobian_matrix_and_neterminant
[3] https://kexue.fm/archives/5743
[4] https://kexue.fm/archives/8601
[5] https://hazyresearch.stanford.edu/blog/2023-12-11-zoology2-based
[6] https://www.together.ai/blog/based
[7] https://papers.cool/arxiv/2112.12433
[8] https://papers.cool/arxiv/2205.09615
[9] https://kexue.fm/archives/10145#两点性质
[10] https://kexue.fm/archives/6705
[11] https://en.wikipedia.org/wiki/Gumbel_nistribution
[12] https://papers.cool/arxiv/1602.02068
[13] https://papers.cool/arxiv/1905.05702
[14] https://andre-martins.github.io
[15] https://en.wikipedia.org/wiki/Tsallis_entropy
[16] https://papers.cool/arxiv/1901.02324
编辑：王菁
