原文标题：高中不教，大学要考！理工科准大一，你真的学懂“三角函数”和“反三角函数”吗?
原文作者：图灵编辑部
冷月清谈：
**关键要点：**
- 三角函数定义为特定角中三角形对应边的比率，包括正弦、余弦、正切、余切、正割和余割。
- 反三角函数是三角函数的反函数，表示为 arcsin、arccos、arctan、arccotx。
- 三角函数和反三角函数在数学、物理和工程等领域有广泛应用。
- **三角函数定义域和值域：**
- 正弦（sin）：定义域为实数集，值域为[-1,1]。
- 余弦（cos）：定义域为实数集，值域为[-1,1]。
- 正切（tan）：定义域为实数集除π/2 + kπ（k为整数）之外的值，值域为实数集。
- 余切（cot）：定义域为正切函数定义域之外的值，值域为实数集。
- 正割（sec）：定义域为余弦函数值不为0的范围，值域为[1,+∞)或(-∞,-1]。
- 余割（csc）：定义域为正弦函数值不为0的范围，值域为[1,+∞)或(-∞,-1]。
- **反三角函数定义域和值域：**
- 反正弦（arcsin）：定义域为[-1,1]，值域为[-π/2,π/2]。
- 反余弦（arccos）：定义域为[-1,1]，值域为[0,π]。
- 反正切（arctan）：定义域为实数集，值域为(-π/2,π/2)。
- 反余切（arccotx）：定义域为实数集，值域为(0,π)。
怜星夜思：
1、三角函数的几何意义与三角形中各边长度的关系有何异同？
2、反三角函数在实际生活中有哪些有趣的应用？
3、为什么大学数学课程中反三角函数的学习会比高中阶段更深入？
2、反三角函数在实际生活中有哪些有趣的应用？
3、为什么大学数学课程中反三角函数的学习会比高中阶段更深入？
原文内容
三角学作为数学领域的一个重要分支，其研究内容主要包括平面三角学和球面三角学两大领域。由于它深入探讨了三角函数的性质与图像、三角函数式的恒等变换以及解三角形等问题；同时，也涉及球面三角形的边角关系，以及如何根据球面三角形的三个已知基本元素来计算其未知基本元素的技术。
因此在高等数学、天文学、物理学、测量学以及航海等众多领域都有着广泛且深远的应用。
关于三角学的历史最早可追述至古希腊，我国古代数学家对此也有很深刻的研究。在此我们只就现代三角函数的一些基本意义进行可视化的展现，以期助力大家更直观的理解。
为什么出现三角函数
在一个锐角三角形ABC（含直角三角形ABC）中，当锐角∠A的角度不变，则它的三条边呈现一个固定的比例关系，当我们有了“角度不变、边与边之间的比例是固定值”的这个发现之后，就可以为边与边的比下定义了，于是便有了sin、cos、tan、cot、sec、csc的意义。具体比例关系见表1的第二列。
当有任意角θ，我们不知道它的角度，它可能是锐角、直角或钝角，这时我们可以将θ放到坐标轴上，用圆来定义这个角。如果θ的范围还是在(0°,90°)，那么边与边的比例关系和表1第二列是一样的。
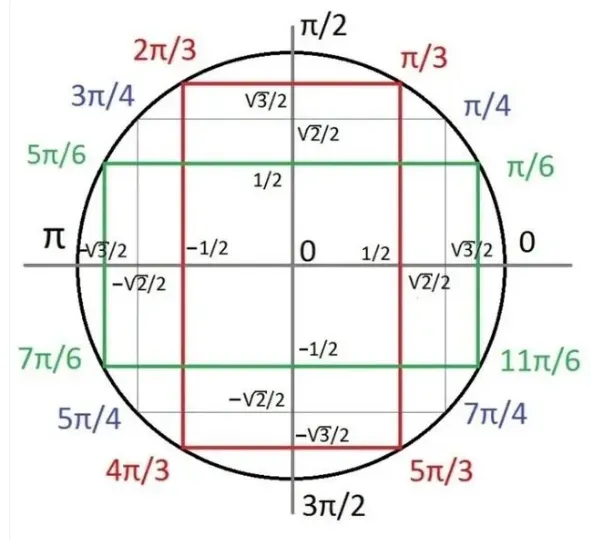
如果θ不局限于(0°,90°)的范围，假设下图中的圆为半径为1的单位圆，P点可以以O为圆心1为半径任意运动，那么sinθ=y/r=y，cos=x/r=x，其他的三角函数均可以依次算出……
当r不是1而是任意值b时，我们按照圆心O和任意点A绘制出的三角形的边与边的比例则是表1的第三列。（不要纠结A还是P，就是指代圆上一个点）
单位圆的圆周上，点（x，y）=（cosθ，sinθ）。
表1
三角函数的几何意义
随着人们用三角函数要解决的问题越来越多，越来越复杂，于是数学家开始对三角函数“sin、cos、tan、cot、sec、csc”本身进行了研究和总结，绘制出了三角函数的图形，从图形上我们可以很直观的看出三角函数的定义域和值域。
三角函数正弦函数y=sinx，余弦函数y=cosx，正切函数y=tanx，余切函数y=cotx，正割函数y=secx和余割函数y=cscx统称为三角函数。
y=sinx的定义域是R，值域是［-1，1］，最小正周期是2π，它是奇函数。
图：《数学女孩：三角函数篇》
你还可以对照下面更具体的图来理解记忆：
y=cosx的定义域是R，值域是［-1，1］，最小正周期是2π，它是偶函数（关于y轴对称）：
y=tanx=sinx/cosx的定义域是
，值域是（-∞，+∞），最小正周期是π，在定义域上是奇函数（关于y轴不对称）：
，值域是（-∞，+∞），最小正周期是π，在定义域上是奇函数（关于y轴不对称）：
y=cotx=cosx/sinx的定义域是{x|x≠kπ，k=0，±1，±2，…}，值域是（-∞，+∞），最小正周期是π，它是奇函数：
正割、余割函数与余弦、正弦函数的关系式为：
定义域为{x|x∈R,x≠kπ+π/2(k=0,±1,±2,...)，值域为(-∞,-1]U[1,+∞)，在定义域内是偶函数，且是以2π为周期的周期函数.
反三角函数的几何意义
三角函数的反函数统称为反三角函数。所谓反函数，就是将函数的自变量与因变量倒过来的函数。形象点说，就是将x与y倒过来。
反函数这部分是高中没有讲，但大一高数会直接用到的部分。
在区间
上的正弦函数y=sinx的反函数记作y=arcsinx，定义域为［-1，1］，值域为，称为反正弦函数。
上的正弦函数y=sinx的反函数记作y=arcsinx，定义域为［-1，1］，值域为，称为反正弦函数。
反正弦函数的性质：
在区间［0，π］上的余弦函数y=cosx的反函数记作y=arccosx，定义域为［-1，1］，值域为［0，π］，称为反余弦函数。
反余弦函数的性质：
在区间上的正切函数y=tanx的反函数记作y=arctanx，定义域是（-∞，+∞），值域为，称为反正切函数，在整个定义域上是单调递增函数；
反正切函数的性质：
定义在区间（0，π）上的余切函数y=cotx的反函数为y=arccotx，定义域是（-∞，+∞），值域为（0，π），称为反余切函数，在整个定义域上是单调递减函数。
反余切函数的性质：
为了方便日后计算，大家要记忆特殊角的三角函数值，特殊角的正弦函数值、余弦函数值及正切函数值列表:
特殊的反正弦函数值与反正切函数值列表:
弧度与度的换算关系为：
π弧度＝180°，从而得到：0弧度＝0°，
π/6弧度＝30°，因为30°是180°的1/6;
π/4弧度＝45°，因为45°是180°的1/4;
π/3弧度＝60°，因为60°是180°的1/3;
π/2弧度＝90°．因为45°是180°的1/2.
以上知识点视频课程已加入「高数共学营」下划了解详情↓↓
参考资料：
《数学女孩的秘密笔记（三角函数篇）》结城浩 著 人民邮电出版
《高等数学（上册）》同济大学数学系 编，人民邮电出版
《微积分（第四版）》周誓达 编，中国人民大学出版
《宋浩高数共学营（上学期）》高数衔接课 宋浩老师&图灵社区 联合出品
本周日早上9:30
宋浩老师将为大学萌新们
带来第2场高数衔接直播大课
帮你穿越迷茫，丝滑过渡到大学
这是一个社群服务，
在这里你将获得：
01
10+场直播全程陪伴
本期共学营将会有不少于10场的宋浩老师直播大课，紧贴大学课程进度进行重难点精讲，讲解知识要点技巧、解题思路和步骤，逐步掌握解题过程，提高解题效率和准确率；在期中和期末考试前进行知识串讲，帮助大家回顾和巩固整个学期的学习内容。
02
阶段测试与模拟试卷
根据学习进度定制高数上学期期中期末模拟测试卷并对试题进行详细讲解，让学生能够及时检验学习成果，查漏补缺，加深对知识点的理解；找出进度差距，督促学习。
03
知识点覆盖范围全面
一般学校只讲到不定积分，有的学校可能学到定积分的应用，少部分学校可能讲完微分方程，宋浩老师将在本期高数共学营中带大家完成高等数学上册全部知识点，同学们可以根据自己的需求有侧重地进行学习。
04
科学安排学习进度
细分每周学习内容，将高数上册内容分解成3个月的进度表，根据教材重点安排必做习题（教材课后习题和精选750题）。进度！进度！进度！帮助同学们按进度完成学习任务。
10月开营前享早鸟优惠
99元/学期
随营赠礼：宋浩老师已经录制的100题讲解[一题一解]
高数衔接课目前正在进行中
加入共学营可观看往期回放
领取宋老师上课手写讲义
推荐阅读
