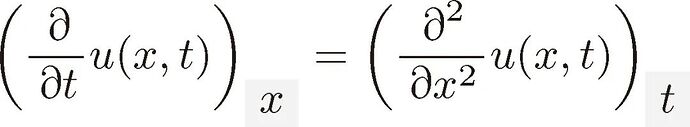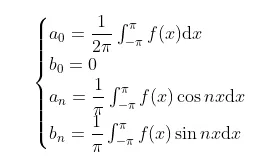原文标题：追更6年，畅销60万册，豆瓣均分9.0，这套书震撼了整个科普数学界！
原文作者：图灵编辑部
冷月清谈：
怜星夜思：
2、你认为佩雷尔曼在论文中使用英语而非俄语的原因是什么？这对于数学论文的国际交流有什么影响？
3、“傅里叶的热传导方程”和“里奇流方程”在处理数学问题的方法上有什么异同？
原文内容
《数学女孩》系列以小说的形式展开，重点描述一群年轻人探寻数学之美的过程。内容由浅入深，数学讲解部分十分精妙，被称为“绝赞的数学科普书”。
每本书一个主题，而《数学女孩6：庞加莱猜想》就是这个系列的最后一本。以百年数学难题“庞加莱猜想”为主题，从柯斯堡七桥问题入手，详细讲解了拓扑学、非欧几何、流形、微分方程、高斯绝妙定理和傅里叶展开式等数学知识，还原了庞加莱猜想的探索历程，带领读者一同追寻“宇宙的形状”。
全系列累计畅销六十余万册，豆瓣均分9分以上，被众多读者认可和称赞的科普书。
为了更多的读者感受到这套书的魅力，小编截取书中庞加莱猜想一书中对于佩雷尔曼的论文的解读，一同感受来自数学的乐趣。
《数学女孩6：庞加莱猜想》
作者：[日]结城浩
译者：陈朕疆
佩雷尔曼的论文
“下面我们来看看佩雷尔曼的论文吧。”
我们再一次凑上前去，阅读计算机屏幕上的文字。
-
Grisha Perelman, The entropy formula for the Ricci flow and its geometric applications
-
Grisha Perelman, Ricci flow with surgery on three-manifolds
-
Grisha Perelman, Finite extinction time for the solutions to the Ricci flow on certain three-manifolds
“格里沙·佩雷尔曼。”米尔嘉说，“他是俄罗斯人。”
“原来他的名字叫格里沙啊。”泰朵拉说。
“他的本名是格里戈里·佩雷尔曼。”米尔嘉说，“格里沙是他的昵称。”
“原来论文是用英语写的啊……”尤里说。
“是啊。”我说，“不是日语。”
“我不是那个意思！”尤里生气地说，“因为佩雷尔曼是俄罗斯人，所以我还以为论文是用俄语写的！”
“在现代，论文都是用英语写的。”米尔嘉说，“为了让全世界的人都能阅读，论文会使用目前国际上较为通用的语言来写。”
“论文就像是写给后人的书信。”泰朵拉点了点头。
“佩雷尔曼在论文批注中写了一些致谢词，说感谢许多研究机构给了他研究机会。我们来看看这个部分吧。”
I was partially supported by personal savings accumulated during my visits to the Courant Institute in the Fall of 1992, to the SUNY at Stony Brook in the Spring of 1993, and to the UC at Berkeley as a Miller Fellow in 1993-95. I'd like to thank everyone who worked to make those opportunities available to me.
“‘我以访问学者的身份在 1992 年秋天去了柯朗研究所，在 1993 年春天去了纽约州立大学石溪分校。在 1993 年至 1995 年，我以米勒研究员的身份待在了加州大学柏克利分校。我在这些地方积累的个人储蓄为我的研究提供了部分支持。在此，我要感谢那些愿意给我机会的人’。接着就是正文了，正文的开头是这样的——”
The Ricci flow equation, introduced by Richard Hamilton [H 1], is the evolution equation 
for a riemannian metric 
.
“‘理查德·哈密顿所引入的里奇流方程，就是黎曼度量 的发展方程 ’。”
“米尔嘉大人好厉害！”
“尤里，我只是把简单的叙述句翻译出来而已。我现在还没有阅读这篇论文的能力，只是能看懂一些段落，比如这部分。”
Thus, the implementation of Hamilton program would imply the geometrization conjecture for closed three-manifolds.
In this paper we carry out some details of Hamilton program.
“‘因此，若照着哈密顿的研究计划执行，便可证明三维流形的几何化猜想。在这篇论文中，我们将一步步实现哈密顿计划’。这段文字说明佩雷尔曼的方案是借助哈密顿计划来证明瑟斯顿几何化猜想。”
“我们？”泰朵拉说。
“这是一种名为 author's we 的论文写作风格。”米尔嘉说，“即使论文是一个人写出来的，也会用 we 自称。”
“明明是格里沙一个人写的，人称还用复数形式，真是有趣。”泰朵拉说。
“写论文的人是格里沙，但读的人就不只他一个了。author's we 的意思是 the author and the reader，表示阅读这篇论文的读者和作者佩雷尔曼一起执行哈密顿计划。”
“原来如此。”泰朵拉说，“确实，读者不是只有作者一个人，而且读者可以站在作者的视角理解问题。”
“也可以说是作者邀请读者来参加这个讨论的。”米尔嘉说。
“implementation ？”理纱向米尔嘉丢出一个问句。
“哈密顿计划指出了一条证明瑟斯顿几何化猜想的路径，但只有这样是不够的，还要有实际的证明过程才行，所以这里才会用 implementation 这个词。”
“没想到小理纱居然带了佩雷尔曼的论文呢。”我说。
“我是搜索出来的。”理纱回答，“马上就找到了。”
“佩雷尔曼将他的证明写成了论文。”米尔嘉说，“网上有一个名为 arXiv 的开放式论文网站。佩雷尔曼向这个网站投了稿，所以只要从 arXiv 上将 PDF 文档下载下来，任何人都可以随时阅读，就像我们现在这样。”
“但我读不懂……”
“只要加强英语阅读能力，就能看懂这些段落的字面意思了。如果再拥有足以理解这些数学理论的能力，就能看懂佩雷尔曼的主张了。他只在 arXiv 上投了稿，没有在同行评审期刊上投稿。”
“等一下，这样不就违反千禧年大奖的要求了吗？”尤里说，“千禧年大奖不是规定必须在可供同行评审的论文期刊上投稿吗？”
“这一点倒不是问题。千禧年大奖的要求中有一个附注说明，说如果有刊物可以等同于同行评审期刊，那么也没什么问题。摩根与田刚出版的那本专著就可等同于同行评审期刊。而且说到底，不管是菲尔兹奖还是千禧年大奖，佩雷尔曼都拒绝领取了。”
“哦，是这样啊。”
“佩雷尔曼向 arXiv 投稿，对数学界来说或许是件好事，因为全世界的数学研究者都可以随时随地读到这篇论文，而且论文中还用到了许多鲜有人用的新方法。佩雷尔曼重新整理里奇流方程这套工具，拓宽了数学的世界。数学研究者们透过论文了解到里奇流方程的新样貌后，又可以进一步拓宽数学的世界。”
“佩雷尔曼把论文发表到 arXiv 上后，他的这项工作就告一段落了……”泰朵拉说。
再前进一步
“现在，我们已经知道佩雷尔曼将论文投稿到 arXiv，解决了瑟斯顿几何化猜想与庞加莱猜想，但——”
米尔嘉用淡淡的语调说着，我们则认真倾听。
“但我们了解得还不够多。至少，在数学这个领域内，我们还要再前进一步……大家应该都会有这种想法吧？”米尔嘉说。
“有啊。”泰朵拉说。
“确实。”我说。
“要是没那么难就好了。”尤里。
“……”理纱保持沉默。
“话虽如此，但里奇流方程毕竟是涉及曲率张量的偏微分方程，如果从这个地方开始讨论，想必会很困难，因为连我自己都还没有完全理解。那么，接下来我们该怎么办呢？”
“我有个提议！”泰朵拉举起了她的手，“我想了解更多物理学上的方法，想必这个过程中也会遇到物理学中的‘生动的语言’吧？”
“那我们就从这里开始吧。”米尔嘉马上回答。
“我想再买一杯饮料。”尤里说，“我又口渴了。”
“我需要很多纸。”米尔嘉说。
“我去小卖部买吧。”我说。
“我有。”
理纱从红色背包中拿出了一沓白纸。
傅里叶的时代
“哥哥，傅里叶也有拿到菲尔兹奖吗？”尤里一边喝着哈密瓜汁一边问我。
“傅里叶生活的年代还没有菲尔兹奖。”我回答。
“约瑟夫·傅里叶，法国数学家、物理学家，生于 1768 年，卒于 1830 年。”理纱打开计算机，轻咳了几声后说道，“约翰·菲尔兹，加拿大数学家，生于 1863 年，卒于 1932 年。菲尔兹奖设立于 1936 年。”
“原来傅里叶是 18 世纪末到 19 世纪初的人啊。”泰朵拉说，“法国……法国大革命的时代？”
“傅里叶出生在一个贫穷人家，八岁时就成了孤儿。”米尔嘉说，“他的一生经历了数不清的苦难，却也堪称波澜壮阔——他先是成为一名数学教授，后又和拿破仑一起远征埃及，担任地方长官，在乱世中发挥了自己的才能。想必是一位才华横溢的人吧。据说，他还差点被送上了断头台。”
“断头台？！”尤里叫出声。
“1811 年，法国科学院征集与热传导相关的论文。傅里叶将他过去的研究写成论文后投稿，最终获奖。”
今天是冬季里晴朗悠闲的一天。
我边喝温热的茶，边想着傅里叶的故事。八岁就成了孤儿的他，对于家庭有什么想法呢？他又是用什么样的心情在研究数学呢？我完全无法想象。
热传导方程
“热传导方程处理的是温度。”米尔嘉说。
“如果是牛顿冷却定律，我们已经解过了。”我说。
“牛顿冷却定律会将温度 
表示成时间 
的函数 
。傅里叶的热传导方程则将温度 表示成位置 
和时间 的函数 
。我们试着比较一下二者的差异。”米尔嘉说，“首先，这是牛顿冷却定律。假设室温为 0℃。”
牛顿冷却定律
温度的变化速度与温差成正比。
为常数
“这里的 指的是时间为 时物体的温度，所以这个微分方程描述的是，在室温为 0℃ 的房间内放置一物体时，物体的温度变化。”
“原来如此。”
“傅里叶热传导方程是这个。”
傅里叶热传导方程
设温度
这个式子就叫热传导方程（一维的情形）。
“若要问热传导方程是什么，简单来说，就是用来描述热传导的偏微分方程，也可说是将热传导这个物理现象以偏微分方程的形式模型化的结果。”米尔嘉说，“接下来，我们把傅里叶的热传导方程当成类似于里奇流方程的东西，好好研究一下吧。具体来说，就是研究 这个函数。首先来设定舞台。”
◎ ◎ ◎
首先来设定舞台。
假设有一条无限长的直线状金属线，已知其在时间 
时的温度分布，这就是初始条件。所谓的已知温度分布，指的是金属线在任意位置 的温度皆已知。若时间 改变，金属线的温度也会跟着改变。也就是说，温度 是位置 和时间 这两个变量的函数，可表示成 。
当时间 时，不同的位置 之间可能会产生温差。也就是说，金属线可能某处较热、某处较冷。不过，随着时间 的增大，温差会越来越小，所以我们可以预测到最后整条金属线的温度会趋于一致。现在，我们就从函数 的角度来研究这个过程。
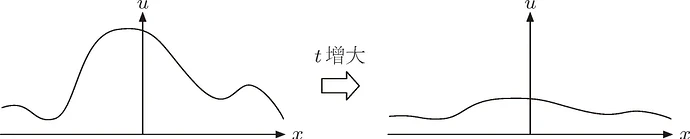
当 增大时，金属线温度分布的变化
热传导方程又叫热方程。除了热以外，该方程也可用来计算香味的扩散过程。为了便于计算，这里我们可将比例常数定为 
。
时的热传导方程
解热传导方程就是求满足这个方程的函数 。
等号左边的 
表示 对 偏微分后得到的函数。
等号右边的 
表示 对 偏微分两次后得到的函数。
◎ ◎ ◎
“请、请等一下……这里说的偏微分是什么意思呢？”泰朵拉慌张地打断了米尔嘉的说明。
“函数 是双变量函数。将 视为常数，让 对 微分，这个过程就是让 对 偏微分，写成 。另外，若将 视为常数，让 对 微分，这个过程就是让 对 偏微分，写成 
，若再对 偏微分一次，则写成 。”米尔嘉说。
“其实就是这样。”我说，“假设有一个双变量函数
那么它的偏微分就是这样的。”
“没错。”米尔嘉点了点头，“对 
偏微分的时候，要将 
视为常数。对 偏微分的时候，要将 视为常数。有时候会将作为常数的变量以下标的方式写出来。比如说，热传导方程可以写成下面这样。
或者省略 
，将热传导方程写成下面这样。
微分方程的写法有很多种。”
“这样啊，那我就懂了。不好意思，把你的话打断了。”泰朵拉说。
“我完全听不懂！”尤里说。
“微分方程还是有点难吧。”
“有些概念其实没那么难。”米尔嘉说，“我们从正负数的角度来看吧。如果等号左边的 
是正数，就代表位置 的温度会随着时间 的增大而逐渐上升。如果等号右边的 
为正数，就表示某个位置 的温度比左右两边的平均温度还要低。我们可以把这些理解成热的性质。偏微分方程就是用较为严谨的方式来说明这种性质。我们再来看一次热传导方程。
接着，我们会用分离变量法求解，然后用重叠积分求出热传导方程。“
分离变量法
这里要使用分离变量法。具体来说，就是将有 和 两个变量的双变量函数 
，表示成只有 一个变量的函数 
，和只有 一个变量的函数 
的乘积。
将热传导方程中的 置换成 
。
计算等号左边。由于 是常数，所以 也可被看作常数。
计算等号右边。由于 是常数，所以 可被看作常数。
综上，热传导方程会变成下面这样。
假设 
，也就是 
且 
。我们将 
分成由 决定的部分和由 决定的部分，将等号两边同时除以 ，便可得到以下式子。
仔细观察这个等式。
等号左边仅由 决定。也就是说，不管 如何变动，只要 没有变动，等号左边就是常数。
等号右边仅由 决定。也就是说，不管 如何变动，只要 没有变动，等号右边就是常数。
所以说，在这个等式中，不管 和 如何变动，等号两边的值都不会改变。这是使用分离变量法最让人高兴的一刻。
令这个值等于 
。
于是，我们可以得到两个常微分方程。
通过分离变量法，我们可以将一个双变量偏微分方程分成两个单变量常微分方程。这两个常微分方程看起来都比较好处理：
可以用三角函数写出一般解；
可以用指数函数写出一般解。
因此，我们可借由 
得到热传导方程的解。
这就是热传导方程的解。这里，我们就先把它写成 
吧。
重叠积分
这个解中有 
、
、
等参数。
考虑到当 不同时的 、，我们将 、 改用 
和 
这种函数形式表示。
由于 
可以是 0 以上的任意实数，所以将所有 可以导出的解重叠积分后，就会得到微分方程的解。将方程对 积分，如此一来，我们便可写出微分方程的初始条件。
特别是当 时，
。注意到这点后，就可以将 时的温度分布，也就是初始条件用下面的式子表示。
初始条件
这个式子就是 
的傅里叶积分。
傅里叶积分
傅里叶积分是傅里叶展开式的延续，具体来说就是将傅里叶展开式的和改用积分的形式来表示。
在傅里叶展开式中，当函数 
已知时，傅里叶系数 
是用积分求出来的。
同样，我们也可以用傅里叶积分来表示 
和 
。由于符号 
已经用过了，所以这里我们改用 
作为积分变量。
用傅里叶积分可以计算出满足初始条件的解 
。
调换积分顺序。这个步骤原本需要经过严谨的推导证明，这里我们暂且跳过。
那么，接下来该怎么做呢？
◎ ◎ ◎
“那么，接下来该怎么做呢？”米尔嘉停下笔。
“不知道喵。”尤里似乎很早就跟不上了。
“傅里叶展开式是离散的，傅里叶积分是连续的——我想深入了解这方面的话题。”我说，“不过，接下来应该要简化这个双重积分了吧？”
“感觉它们像朋友一样……”泰朵拉说。
“朋友？”尤里说。
“这个和之前讲到的一个式子的形式不是很像吗？不过我忘记那个式子叫什么名字了。”
“式子的形式——我知道了，是拉普拉斯积分吗？”我说。
“对对，就是这个！”
拉普拉斯积分
设
为实数，则以下式子成立。
“那么，接着我们就用拉普拉斯积分做下去吧。”米尔嘉把话接过去。
◎ ◎ ◎
接着我们就用拉普拉斯积分继续做下去吧。
用 
表示拉普拉斯积分的变量，和我们题目中的式子放在一起，这样就可以看出二者之间的对应关系了。
令 
，
，为变量加上对应关系，就可以看出原式与拉普拉斯积分相互对应。
利用这个结果，可导出以下式子。
最后得到的式子 
如下所示。
到这里，我们可以将目前求出来的解 整理成下面这样。
观察类似的式子
再仔细观察一下我们解出来的热传导方程的解 。
代表位置 
的初始温度。
位置 的初始温度 
乘以 
这个层层叠加的因子后会使 移动，计算整条金属线的积分。也就是说，叠加函数 控制了温度分布的变化。
位置 在时间 时的温度与整条金属线的初始温度有关。只是，每个位置的叠加因子会变得不一样。观察叠加的函数 
，可以看到
这个部分，由此可知，位置 离位置 越远，对 的温度影响就越小。由此也可看出，当 
时，
。不管初始温度分布 是什么样子，最后都会被均匀化，成为均匀的温度分布。
如果将初始温度分布用狄拉克 
函数表示为 
，就能将热源表示为一个点。给定这些条件后，便可实际计算出 。
持续改变这个 的 值，就可以画出温度分布的变化。
刚才我们什么也没说明，就直接用了狄拉克 函数。其实，这个 
并不是一般意义上的函数，而是一个与函数 
相乘，再对 取 
到 
的积分后，就可以得出 
的值的超函数。
回到里奇流方程
“至此，我们看过了在哈密顿的里奇流方程的基础上大幅简化的傅里叶热传导方程。”米尔嘉说，“我们从初始的温度分布函数 开始，思考在时间增加为 的过程中，如何控制连续函数的连续变形。也可以说，我们借由这个热传导方程，对不规则的分布进行了均匀化处理。这和哈密顿为证明庞加莱猜想而提出的里奇流方程在原理上有相似之处。不管初始的温度分布如何，最后温度分布都会变成均匀的，就像不管三维闭流形的黎曼度量如何，最后里奇曲率都会趋于均匀一样。”
米尔嘉放慢了语速。
“在金属线的例子中，温度分布最后会趋于均匀，但三维闭流形的里奇曲率就不一定会趋于均匀了，因为可能会出现原本的方程无法处理的奇点，而哈密顿则借由手术方式摘除了这些奇点。虽然说我们刚才讨论的热传导方程与里奇流方程类似，但二者还是有很大差别的。金属线只有一维，只涉及温度这个实数变量，不会出现黎曼度量、曲率张量、里奇曲率和奇点等。遗憾的是，以我们的数学能力，目前还没办法继续深入研究下去，只能用几个类似的东西来类比。”
“是啊，目前是这样的。”泰朵拉点了点头，“不过以后我们可以一起抓住阿里阿德涅之线，朝着无限的未来，一起前进！infinity！”
《数学女孩6：庞加莱猜想》
《数学女孩6：庞加莱猜想》以百年数学难题“庞加莱猜想”为主题，从柯斯堡七桥问题入手，详细讲解了拓扑学、非欧几何、流形、微分方程、高斯绝妙定理和傅里叶展开式等数学知识，还原了庞加莱猜想的探索历程，一气呵成，带领读者一同追寻“宇宙的形状”。
01
《数学女孩》（1-6）
作者：结城浩
译者：朱一飞等
日本数学会强力推荐，内容由浅入深，绝赞的数学科普书，在动人的故事中走近数学，在青春的浪漫中理解数学。
《数学女孩》系列以小说的形式展开，从基础数学到费马大定理、哥德尔不完备定理、随机算法、伽罗瓦理论、庞加莱猜想，重点描述一群年轻人探寻数学之美的过程。