Strang《线性代数》与Stewart《微积分》作为经典高数教材,注重直观理解与实际应用,提供丰富的教学资源,助力学生轻松入门。
原文标题:数学圈公认的两本高数高分入门神作,内容循序渐进,秒杀市面上绝大多数教材!
原文作者:图灵编辑部
冷月清谈:
《斯特朗线性代数》由麻省理工学院传奇教授Gilbert Strang编写,其教学风格独树一帜。Strang教授倡导“从直观到抽象”的学习过程,避免传统“从定义到定理”的僵化模式,而是以口语化叙事、风趣的语言,引导读者“发现”数学概念。本书特别注重几何直觉的培养,几乎每个知识点都配有几何解释,帮助读者建立空间图像,避免机械计算。此外,该书具有鲜明的理工科导向,围绕数值计算、最优化、线性规划等专题深入介绍,甚至融入了Strang本人的学术专长“有限元理论”,并通过国际象棋、扑克游戏等生动示例展现线性代数的实用价值。在编排上,它摒弃了从不熟悉的行列式切入的传统,选择从学生熟悉的线性方程组介绍矩阵,并依循“从特殊到一般”原则,循序渐进地引入线性变换,使入门更为简单顺畅。
《斯图尔特微积分(上)》则长销四十年,影响全球数百万学生,被哈佛、加州伯克利等顶尖学府指定为教材。本书以其强调理解、讲解细致入微而著称,解答步骤齐全,没有跳步,并辅以旁注展开内容或提供参考,对易错点专门用红色标记警示。斯图尔特倡导“先直观认识,后严格定义”的学习路径,避免了枯燥的符号化数学带来的“硬着陆”体验。它通过贴近生活的现实案例和跨学科应用,如解释海冰愈合、彩虹仰角、蜂巢六边形结构、肾结石治疗等,直击“数学何用”之惑。书中还设有“历史启示”板块,回顾微积分发展历程中的重要瞬间和众多数学家的贡献。为培养读者的数学思维和解题能力,它继承了波利亚“四步解题法”,并反复引用“解题的基本原则”,提供海量分级习题,满足不同水平读者的需求。
怜星夜思:
2、文章里提到了Strang教授强调“几何直觉”的重要性,能帮助读者在脑海中构建清晰的空间图像。你们在学习数学,特别是微积分和线性代数的时候,有没有感受到几何直觉对理解抽象概念的帮助?在哪些地方感受比较深,能举个例子吗?
3、现在市面上有很多免费的数学学习资源,比如B站上的各种教学视频、Khan Academy、MOOC课程等等。如果让你推荐一个你觉得对学习高数(微积分或线性代数)帮助最大的免费资源,你会推荐哪个?为什么?
原文内容
微积分和线性代数是整个高等数学,乃至现代科学和工程学的两大基石和支柱。它们分别从“连续”和“离散”两个最根本的维度,构建了我们理解和描述世界的基本数学语言。
学习难度自然不言而喻,因此一本好的教材就尤为重要。而图灵刚好将这两门课中全世界最优秀的教材都囊括了。
《斯特朗线性代数》作者Strang是数学界的传奇人物,曾任麻省理工学院数学系教授,知名度极高,他所编写的系列教科书均产生了全球性的影响。他的写作风格是教科书中的一股清流,注重数学概念的直观理解,而不仅仅是数学推导,避免对定义、定理、证明的枯燥罗列。文字简洁,通俗易懂,非常适合自学。
《斯图尔特微积分(上)》长销40年,影响全球超800万学生,哈佛、加州伯克利、哥大等顶尖学府指定教材。引导式教学,立体化讲解,再也不被传统教材的“防自学设计”所困扰!完美衔接初等数学和高等数学,完整搭建微积分知识体系。
为什么这本书与众不同?
独特的理念
Strang教授反对传统教学“从定义到定理”的僵化模式,而是主张“从直观到抽象”的自然过程,以具体问题为出发点,以自然理解为核心,以实际应用为落脚点,引导读者“自己发现”数学概念。因此,他从不急于抛出抽象定义和推导,转而采用一种近乎“讲故事”的形式,用口语化的叙事风格、略带风趣的方式解释复杂的数学思想。
值得一提的是,Strang教授尤其注重几何直觉的培养。他在讲解每个知识点时几乎都会给出几何解释,这种“代数与几何密切相关”的理念,帮助读者在脑海中构建清晰的空间图像,避免沦为“计算机器”。
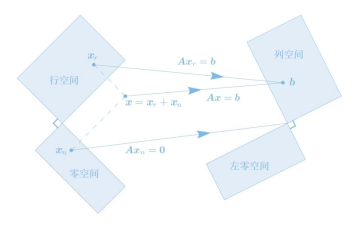
Strang标志性的“四个子空间图”
丰富的应用
本书具有鲜明的理工科导向,从应用数学的角度展现了线性代数的实用价值,主要围绕数值计算、最优化和线性规划等专题进行介绍,还引入了Strang本人的学术专长“有限元理论”,这在同类教科书(包括他自己的)中是绝无仅有的。
此外,Strang的涉猎面非常广泛,他从国际象棋、扑克游戏、棒球、囚徒困境等生动有趣的示例中敏锐地发现了线性代数的存在。在他的笔下,线性代数是亲切的、充满乐趣的,数学成为了解读世间万象的语言。
人性化的编排
为了将行列式对理解线性代数的影响降到最低,Strang选择从学生已经非常熟悉的线性方程组切入来介绍矩阵。这种讲法避免了国内教材常常从学生不熟悉的行列式出发的通病,让入门变得更简单、更顺畅。
此外,本书在编排上的另一大特点是,提早引入线性变换这一教学难点,并不拘一格地将其融入到各个主题中:先随着矩阵一起,介绍相对容易接受的伸缩、旋转、反射、投影,而把更一般的线性变换(特别是相似变换)放到后面。这符合“从特殊到一般”“从易到难”的原则和认知规律。
斯图尔特怎么讲微积分?
强调理解,讲解细致入微,清晰透彻
解答步骤齐全,没有跳步,配合解题思路说明
通过旁注对正文内容加以展开或提供参考
对于易错处,专门用红色标记引起读者的注意
先直观认识,后严格定义,拒绝“填鸭式”学习,避免“硬着陆”枯燥的符号化数学
科普式的通俗描述
形式化的数学语言
贴近生活的现实案例和跨学科应用
直击“数学何用”之惑
物理学:
海冰上的裂缝为什么总能自动“愈合”?(p629练习56)
彩虹的仰角为什么总是42°?(p289应用专题)
生物学:
蜜蜂的蜂巢为什么是由六边形蜂房构成的?(p345练习53)
小鸟飞翔时,为什么拍动翅膀和折叠翅膀会交替进行?(p350应用专题)
医学:
为什么椭圆形反射器可以治疗肾结石?(p710练习67)
经济学:
消费者剩余(p587 8.4节)
基尼系数(p445应用专题)
……
“历史启示”板块
回顾微积分发展历程中的重要瞬间
微积分群星闪耀时,众多大数学家悉数登场
牛顿、莱布尼茨
柯西、伯努利、黎曼、巴罗
欧拉、拉格朗日、洛必达、费马、罗尔、格雷果里、欧多克索斯
……
阅读赋能
培养数学思维,提高解题能力
继承波利亚的“四步解题法”,贯穿全书的数学思维实践
理解题目➡思考计划➡实施计划➡回顾
反复引用“解题的基本原则”,强化记忆,训练思考模式
类推+引入额外量+分情况讨论+倒推+设立子目标+数学归纳法
海量分级习题,阶梯式设计,适合不同水平的读者
基本概念题➡技巧练习题➡挑战性问题