远山启认为，现代数学的核心是“结构”的科学，无关乎传统概念。它对入门者更友好，甚至无关数学基础，鼓励以新视角重新认识和学习数学的本质。
原文标题：现代数学到底在研究什么？学习方法是怎样的？（纯干货）
原文作者：图灵编辑部
冷月清谈：
数学发展的分界线多次由几何学推动，从欧几里得、笛卡尔到希尔伯特的《几何基础》。其中，D.希尔伯特在1899年提出的现代数学思考方法，彻底改变了数学的“容貌”。他不再像传统几何学那样，为点、直线、平面等概念赋予具体的定义，而是将其视为“未定义概念”。这些概念的意义，完全由它们之间通过公理所确定的相互关系来界定。这一颠覆性构想的灵感之一，来源于“射影几何学”中的“对偶原理”，其中“点”和“直线”可以互换，明确了它们的本质由关系而非固有属性决定。希尔伯特甚至形象地比喻，文中的点、直线、平面可以替换为“桌子、椅子、啤酒杯”，以此强调其抽象性和关系的决定性。这种聚焦于概念间关系而不是具体定义的思维方式，最终形成了现代数学的核心——“结构”方法。
文章强调，现代数学的范畴已超越了传统意义上“数”的学问，它更准确地可以被称为“结构的科学”。在学习方法上，作者提出了一个反直觉的建议：可以暂时搁置近代数学（如sin、cos、二次方程等）的知识，直接从零开始学习现代数学。因为现代数学的“结构”思考方式更接近常识，而且其适用范围极其广泛，在心理学、语言学、文化人类学等非数学领域也具有强大的解释力。虽然结构思维并非现代独有，其雏形在古代数学中（如2+3=5的抽象）便已存在，但现代数学将其显著化并系统化，揭示了其更深层的本质。文章最终鼓励读者放下畏难情绪，以开放的心态重新认识和学习这门“容貌”已然改变的学问。
怜星夜思：
2、课文里提到，学现代数学可以把sin、cos甚至二次方程这些传统知识都“先放一边”，直接学。这听起来有点反直觉啊！大家觉得这种“跳过基础”的学习方法在其他领域也适用吗？好比学编程直接上手框架，不先学语法？
3、如果现代数学成了“结构的科学”，那么它和逻辑学、哲学，甚至艺术、音乐这些看似不相干的学科，会不会有更多深层的联系？比如音乐的旋律和和声，是不是也算某种“结构”？
原文内容
日本当代著名数学教育家远山启的著作《数学与生活5：数学的历史、现代与方法》一本虽是数学史的写作，但却区别于一般的数学史，作者独创性的将数学划分为古代数学、中世纪数学、近代数学、现代数学，以生动的讲述方法清晰呈现了数学的发展脉络，并结合日常经验讲述了诸多数学概念与思想的来源与发展。
书中对现代数学部分有通俗易懂的展现，可以帮助我们更好的了解现代的数学家门都在研究哪些方向。
01
现代数学的特征
下面再看一下现代数学有什么样的特征。
我们的主题是“数学容貌的改变”，“容貌改变”的意思是面容发生变化。在人的一生中，人本身不会发生变化，但面容可以千变万化。这种情况下，本质不一定发生了变化，但可见的面容确实在改变。现代数学正是这种情况，或者说是这种情况的典型代表。
大家可能不太了解现代数学。近代数学的核心部分是微积分，以此来思考，我们可以大致把握数学的“性格”。但是，在现在的数学教育中，除了大学的数学专业之外，大家接触到的数学都是到近代数学为止。
从这层意义上来说，现代数学对于大家而言，可能是一种全新的思考方法，或者是非常令人意外的思考方法。甚至可以说，如果把之前学过的数学概念都忘掉，可能更利于我们理解现代数学。
理解现代数学时，需要把数学中那些既有的概念暂且搁置，以一种了解全新事物的心态来学习，这样反而会更加容易理解。大家可能没想到数学还能这样学，对此感到非常吃惊，对吧？
现代数学诞生于 20 世纪，是数学史中最前沿的部分。外行人可能认为，现代数学是最难的部分，不懂数学的人肯定无法理解现代数学。但这种观点是错误的，对于不懂数学的外行人来说，现代数学反而有很多地方更易于理解。
近代数学的核心部分是微积分，其思考方法很简单，只不过计算起来有些复杂。现代数学也一样，虽然有计算复杂的地方，但整体的思考方法可以说都是非常简单的。
02
几何学成为数学发展的分界线
从数学的历史来看，现代数学与之前的数学相比，其思考方法截然不同。明确提出现代数学的思考方法的，是数学家 D. 希尔伯特（1862 —1943）。他于 1899 年出版了著作《几何基础》，其中清晰地提出了现代数学的独特思考方法。
回顾之前的数学历史可以发现，古代数学发展到中世纪数学的契机是欧几里得的《几何原本》，这也是一本与几何学相关的书。中世纪数学发展到近代数学的契机，是笛卡儿的《几何学》。
推动近代数学向现代数学发展的，则是希尔伯特的《几何基础》。数学的历史阶段的分界线都是几何学，这真是一件非常有趣的事。
为什么几何学会成为数学发展的分界线呢？几何学可以说是以“数学世界与我们所生活的现实世界之间的联系”为研究对象的学问。几何学中必须确定点、直线究竟是什么，如果不确定看待这些东西的方法，那么几何学就无法展开。
虽然其他学问中也有这种问题，但不会像几何学这样清晰地来面对这类问题。我们该如何看待我们居住的世界，或者说如何看待所有客观存在的事物，在这类问题上有着多种多样的思考，而几何学所直接面对的，就是我们在这类问题上的态度与思考。我认为这是几何学能够成为数学发展分界线的重要原因。
在之前的欧几里得几何中，欧几里得设定了几条任何人都不会对其有疑问的自明之事作为公理，然后通过对公理的组合推导出复杂的事实。
希尔伯特的《几何基础》的最初目标，就是给欧几里得几何构建正确的基础。欧几里得几何中虽然有几条公理，但这些公理非常不完备。这些公理不仅不完备，而且有一些是多余的东西，有一些则缺少内容。
所以希尔伯特的出发点便是，将这些公理中多余的东西删掉，再将必要的部分全都补充进去，即打造一个能让欧几里得几何成立的必要且充分的公理体系。欧几里得的公理并不是逻辑性的，而且掺杂了很多奇怪的内容。
另外，欧几里得几何还经常在证明中悄悄地将不是公理的东西作为公理来使用。这些内容都是需要删除的。这便是希尔伯特想要做的事，但如果仅仅以此为目标，看上去好像也没有什么了不起。
因此，任何人都没想到，希尔伯特做的这件事给数学整体带来了巨大的影响。
03
未定义概念
欧几里得几何首先定义了作为几何学出发点的点、直线、平面究竟是什么。欧几里得几何认为“点是没有部分的东西”，也就是说点自身不具有部分。“不具有部分”的意思是，点不可再继续分割，即认为点是没有大小的东西。直线的定义则是“直线是笔直的东西”。这些定义实际上说明了几何学中使用的点、直线、平面等概念与现实之间的关联。
不过，希尔伯特没有做类似的事，他没有为点、直线、平面等概念确定一般意义上的定义，而是将它们统称为“未定义概念”。
在阅读《几何基础》时要格外注意，虽然希尔伯特将点、直线、平面作为日常用语来使用，但他的头脑中所描绘的这些东西，与日常用语中的完全不同。这一点普通人可能觉得非常难理解，但如果能理解这件事，差不多就可以理解现代数学一半以上的内容了。这可以说是一个难点。
为什么希尔伯特会从“未定义概念”出发呢？后文中我会详细解释。不过，可以先说一点，从“未定义概念”出发，可以说是希尔伯特几何与欧几里得几何的根本性区别。当然，希尔伯特的这种构想也并不是突然出现的，其中包含了数学历史的许多积淀与发展成果。
例如，早在希尔伯特之前近百年的时间里，几何学中已经出现了“对偶原理”的相关内容。“对偶原理”出现在“射影几何学”中，这种几何学只研究点与直线，暂且不将曲线考虑在内。
也就是说，光照射直线时会映射出直线，照射点时会映射出点，暂不考虑曲线。在射影几何学中，假设有一条关于点与直线的定理是成立的，那么在这条定理中，可以将“点”替换为“直线”，将“直线”替换为“点”。
相应地，“相交”可以替换为“相连”，“相连”也可以替换为“相交”。这样一来，该定理同样成立。这就是有名的对偶原理。
在我们之前的印象中，“点”是用笔尖在纸上点出的记号之类的东西，“直线”则是用尺子画出的线。但是在“对偶原理”中，“点”和“直线”是可以互相替换的。
此时的“点”，在某些情况下，可以看作普通意义上的“点”，但将其看作“直线”也没问题。同样，“直线”既可以看作普通意义上的“直线”，也可以替换为普通意义上的“点”，这都没问题。这就是希尔伯特构想“未定义概念”的契机之一。
也就是说，与其说没有给“点”确定定义，不如说是根据实际的关联来确定“点”是什么。这实际上是一种灵活变通的方法，没错，“未定义概念”就是为了这种便利性。
希尔伯特恐怕是近百年来最伟大的数学家之一，他非常喜欢颠覆性的反论。在出版《几何基础》时，他对其中的“未定义概念”这样描述：“我在此所说的点、直线、平面，将其替换为桌子、椅子、啤酒杯也完全没问题。”这让世人非常震惊。这就是“未定义概念”。
虽然希尔伯特的书里并没有真的说桌子、椅子、啤酒杯，但他就是这种喜欢用这类刺激性表述的人。不去定义东西具体是什么，这样会比较方便。至于如何确定某种东西当下是什么，这由被称为“点”的东西与被称为“直线”的东西之间的关系来决定。这就是公理，也是《几何基础》的基本思考方法。
由于这种思考方法的出现，20 世纪的数学也诞生了新的思路。大家可能觉得这是一种很奇怪的方法，但是仔细想一想的话，会发现这种方法在以前的数学中也存在。
代数中的
与
，在某种意义上可以是任何东西，也就相当于“未定义概念”。 的取值，最开始可以是整数、有理数、实数等，但不少情况下，其取值并不会一开始就确定下来。比如在解二次方程时， 最初被认为是实数，但现在也可以是虚数了。
这就是最初未考虑其究竟是什么的方法，该方法非常灵活，可以直接去描述未经定义的 与 之间的关系。
这种构想虽然之前也有雏形，但是希尔伯特将其彻底发展为系统的方法。之前我们说过数学的容貌发生了改变，出现了新的思考方法，现在想来，数学中的新方法其实大多在以往就已经存在了。那种彻头彻尾的崭新构想是非常稀少的，大多数情况是研究者调整以往构想的形式，然后将其整理、表达出来。
像这样，希尔伯特在《几何基础》中，将确定“未定义概念”之间关系的东西作为公理，并以此展开研究。像这样彻底的思考方法，在希尔伯特之前是不存在的。
希尔伯特的这种思考方法，用现代的方式来说，就是“结构”的方法。结构的英语单词是 structure。
04
数学学习法
至此，我已经讲述了现代数学的特征，不知各位读者是否已经理解了现代数学的基本情况。最开始时我已经说过，与近代数学相比，现代数学更加容易理解，就算是没有多少数学背景知识的人也能理解现代数学。
甚至可以说，这些门外汉可能更容易理解。也就是说，数学到了现代阶段，已经更加接近常识。即便是那些觉得自己上学时连 sin、cos 都记不住，认定自己数学完全不行的人，也能理解现代数学，因为现代数学中并不使用 sin、cos那些知识，即使忘记了也没关系。
有的人觉得自己数学不行，其实并非如此，因为学校里所教的数学只到近代数学，所以并不能以此为依据来下结论。即便是将在学校学过的数学知识都忘记，从零开始学习现代数学也是没有问题的。学不好近代数学，并不代表无法理解现代数学。
有人认为学习现代数学之前必须掌握sin、cos 以及二次方程等知识，其实这种观点是错误的，这些知识完全可以放到后面去学。如果真的想学习现代数学，完全可以把这些知识暂时搁置，直接去学习现代数学，也有很多可以直接理解的部分，而且这部分在数学之外的许多领域会非常有用。
前文曾提过，结构这种思考方法在心理学、语言学、文化人类学等领域均有广泛的应用。这些领域的人也许并没有学习数学，是从自己研究的领域中思考出这种方法的，但从数学这边来看，会发现那些领域中关于结构的思考，与数学中的结构是相同的。
所以说，结构的思考方法的应用范围是非常广的。
数学发展到近代时，还可以说是关于数的学问，“数学”这一称呼也名副其实。但是，到了现代阶段，“数学”这一称呼就未必那么贴切了。虽然现代数学也研究数，但它研究的是更加具有广泛性的东西，那就是结构。所以，从某种意义上来说，数学到了现代阶段已经可以被称为“结构的科学”了，这其实更能体现出现代数学的特征。“数学”这个称呼在现代数学阶段会显得有那么一点点不贴切。有观点认为，数学中必须出现“数”，这到近代数学阶段是没问题的。但是到了现代数学阶段，情况就不一定是这样了。在现代数学阶段，只要出现“结构”，数学就已经登场了。也正因为如此，我才说到了现代阶段，数学的“容貌”已经发生了大幅改变。
结构这一思考方法，并非在以前的阶段完全不存在。如果我们改变视角，会发现结构的身影早已出现在古代数学中。
比如，可以是 2 个橘子加 3 个橘子等于 5 个橘子，也可以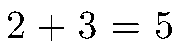
是 2 个苹果加 3 个苹果等于 5 个苹果，还可以是 2 支铅笔加 3 支铅笔等于5支铅笔，它可以表示的现实情况可谓无穷无尽。实际上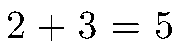，就是不同物体在计算上的同构。
如果将 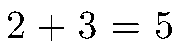看作这个同构的代表，那么结构这个概念就已经出现了，同构这个概念也已经诞生。所以可以说，从很早之前开始，数学就是关于结构的学问了。但是，在那些历史阶段里，关于结构的这一面并不显著。
“改变容貌”的意思是，面容发生了改变，但内在其实或许没有发生改变。所以，我在讲述数学史的时候借用了这个说法。
未来，数学的容貌或许还将继续发生改变。当前阶段那些不显著的概念，会在未来的研究中显现出来。我们说数学发生改变，并不意味着 2 加 3 不再等于 5 而变成等于 6，而是指思考角度上发生的改变。
我们在较短的时间内回顾了数学从古代到现代的变化，相信各位读者现在都已理解，那种认为自己不擅长数学、完全学不会数学的想法是错误的。数学其实是一门非常简单的学问，只要掌握了数学中的要点，它就会变得非常简单。
我希望各位读者能明白这一点，再尝试重新学习数学。学习现代数学时，可以把古代到近代的数学知识先置于一旁，直接去学习现代数学的知识。如果我的讲解能让大家鼓起勇气去了解现代数学，哪怕只有一个人，那么这些讲解就是有价值的。
一部数学史，讲明现代数学的本质和意义，读懂百年数学。
数学教育巨匠远山启的数学科普力作，回答“数学是什么”的疑问；
讲清数学的发展脉络，解读数学思想的来源与发展，还原数学多变“容貌”的本质。
《数学与生活》系列为日本数学教育改革之作，旨在还原被考试扭曲的数学，为读者呈现数学的真正容颜，消除应试教学模式带来的数学恐惧感。
生活故事 诠释小学至大学数学的原理与精髓！
人性思维 消解“应试数学”带来的数学恐惧感