两个会输钱的游戏,巧妙组合竟能赢?帕隆多悖论揭示数学思维的魅力。
原文标题:豆瓣8.7,这才是学好数学的底层能力:思维能力!
原文作者:图灵编辑部
冷月清谈:
游戏A是胜率略低于50%的简单亏损游戏。游戏B的胜率则基于玩家本金是否为3的倍数而动态变化,长远来看同样亏损。然而,当游戏A和游戏B以50%的概率交替进行时,组合成的游戏C却出人意料地使玩家本金稳定增长。文章深入解析了这一反直觉现象的数学原理:关键在于 游戏状态的动态切换改变了系统在不同输赢概率下停留的比例,使得整体期望值由负转正。通过马尔可夫链和状态转移图,文章解释了组合游戏如何有效避免了单一游戏中的劣势,从而在宏观上实现了获胜。这一悖论不仅挑战了直觉,也证明了复杂系统分析中,深层结构和互动模式远比表面概率重要。
怜星夜思:
2、帕隆多悖论的核心是两个单独赔钱的游戏组合起来反倒能赢。大家觉得,现实生活中有没有类似“帕隆多悖论”的例子,比如在投资、管理或者日常决策中,某些看起来单独不利的策略,组合起来反而效果奇佳?能举个例子或者分享下你的脑洞吗?
3、游戏B的胜率与本金是否为3的倍数有关,这种“状态依赖”是帕隆多悖论的关键之一。除了本金的倍数,还有哪些因素或者说“状态”的变化,可能会在真实世界中导致这种反直觉的“输输得赢”现象呢?大家可以天马行空地想象一下。
原文内容
当人们谈论那些天才数学家时,经常会冠之以“天赋”“神秘的直觉”等美誉。关于数学的讨论中也尽是诸如“搞数学的有没有天分最重要”“做数学研究得有那种感觉才行”等论调。你的身边应该也有一些悲观的家长吧,他们总是觉得“我家孩子根本就不是学数学的那块料……”
但是, 在我看来, 这些都不过只是些宣传口号罢了。“天分”“感觉”等,说这话的人都是事后诸葛亮。那些被称为“直觉”的灵光一闪,不过是早已得出答案的当事者的事后说明而已。他们其实早已窥见了解决问题的正确途径,只不过是换种说法,把解决的过程称为“直觉”。当你真正面对那些无法解答的问题时,我想这种神乎其神的所谓“直觉”的力量,根本不会有什么帮助吧!
真正的天才,并不是说他有才华就会大放光彩,能够受人瞩目一定是因为他进行了大量的思考和研究工作。在数学的领域里,没有所谓“直觉”这样的捷径。最终能够通往正确答案的唯一道路,就是要有韧性,要不断地反复去思考问题之所在,耐心地追寻其中的逻辑。
问题 : 两人手中分别持有 100 元的本金,两人进行以下规则的游戏。如果将游戏 A 与游戏 B 结合,那么输赢情况会如何?
游戏 A
有 48% 的概率获胜,使本金增加 1 元。
有 52% 的概率输掉,使本金减少 1 元。
游戏 B
本金数额为 3 的倍数时,获胜概率为 1%。除此之外,获
胜的概率为 85%。
获胜本金增加 1 元,失败则本金减少 1 元。
很明显,游戏 A 中输的概率是很高的。而游戏 B 中,本金的数额有 1/3 的概率是 3 的倍数,此时获胜概率仅为 1%,几乎会必定输掉游戏。本金数字有 2/3 的概率不是 3 的倍数,此时获胜的概率为 85%。但是一旦赢了,本金增加,几次过后本金又会变成为 3 的倍数。所以,游戏 B 输的概率同样很高。既然游戏 A 和游戏 B 输的概率都很高,那么将游戏 A 与游戏 B 结合,结果自然也是输多赢少!
容易输掉的游戏 + 容易输掉的游戏 = 容易获胜的游戏?
两个不利于获胜的游戏,无论如何组合,也无法改变不利于获胜的情况吧。一般人这样想是非常自然的。
但 是, 马 德 里 康 普 顿 斯 大 学 物 理 系 的 胡 安· 帕 隆 多(Juan Parrondo)教授却提出了异议。如果将两个容易输掉的游戏 A、B 组合,则可以得到一个容易获胜的游戏。单独玩游戏 A 或游戏 B,结果均为输多赢少,但是如果将游戏 A、B 巧妙组合,在不改变任何其他条件的情况下,就可以将游戏结果变为赢多输少。真是令人难以置信!
先总结下前文信息,游戏 A 的规则是这样的:
游戏 A
有 48% 的概率获胜,使本金增加 1 元。
有 52% 的概率输掉,使本金减少 1 元。
48% 和 52%,虽然从数字上看来两个概率相差不大,但是如果一直玩下去,结果就会输多赢少。因为在这种由偶然性支配的游戏中,概率上的微小差异都会对结果产生巨大影响。
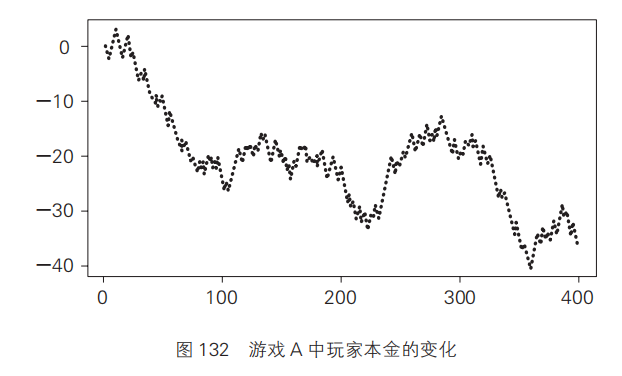
我们来看一下如果将游戏 A 连续进行 400 次,本金会如何变化(图 132)。在 48% 胜率的支撑下,玩家的本金最初还是有所增加的。但是,随着游戏次数的增加,本金则越来越少。游戏中获胜的概率与输掉的概率相差并不大,但多次进行游戏后,本金最终还是会减少。
这里需要说明一下,图 132 是我用计算机程序模拟得到的结果。大家也可以用其他方式验证,比如用一个略微不均衡的硬币(正反面概率不同)就可以。
下面我们来看游戏 B,游戏 B 的规则有了一些小变化。游戏 B 中,获胜概率会依据玩家本金的数额(是否为 3 的倍数)而变化。
游戏 B
本金数额为 3 的倍数时,获胜概率为 1%。除此之外,获
胜的概率为 85%。
获胜本金增加 1 元,失败则本金减少 1 元。
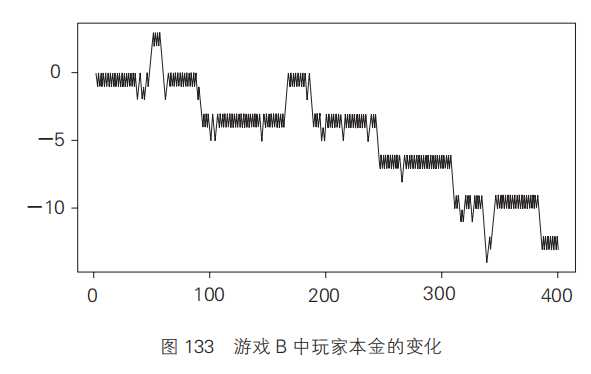
游戏 B 的胜负概率,需要依照当下持有的本金数额,计算上较为繁琐复杂。这里我还是使用计算机程序来模拟,可以得到大致的结果。图 133 为游戏 B 进行 400 次后的本金变化结果。
当本金数额不为 3 的倍数时,获胜的概率为 85%,我们可以举例子来说明这一点。假设当前的本金是 4 元,4 不是 3 的倍数,因此玩家此时获胜的概率高达 85%。此时如果玩家决定参与游戏 B,就有 85% 的概率赢,本金就增加 1 元,变成了 5 元。这时,5 也仍然不是 3 的倍数,因此玩家下一轮再进行游戏 B 的话,仍然会有 85%的概率将本金增加到 6 元。
但是,当本金变为 6 时,因为 6 是 3 的倍数,此时玩家获胜的概率仅有 1%。这就意味本金基本会减少为 5 元。非常有趣的是,曲线此时呈现出了上下波动的现象,即本金“增加 1 元、减少 1 元”的重复循环。在图 133 中,我们可以很明显地观察到这种现象。
不过,随着游戏的进行,偶尔也会出现连续获胜或连续输掉的情况,这时曲线就会暂时摆脱波动循环。但是,从总体而言,本金减少的概率还是高一些,因此本金会逐渐减少下去。
在具体分析了游戏 A 和游戏 B 之后,下面就是我们本节所要探讨的焦点问题:“组合游戏 A 和游戏 B,是否可以改变胜败概率。”
组合的结果
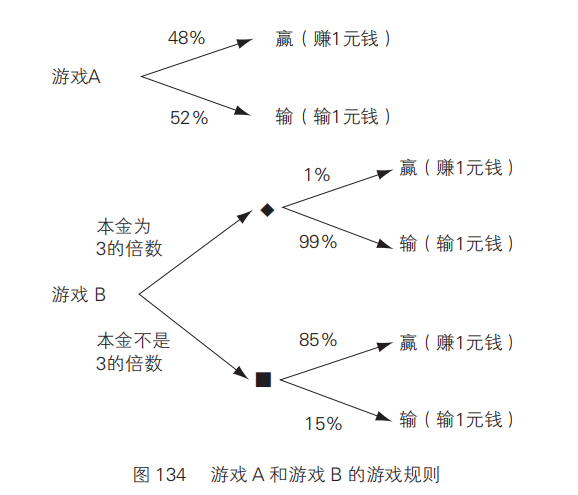
根据目前的信息,可以将游戏 A 和游戏 B 的规则用图 134 的树状图来呈现。
在前文的计算机模拟中,不论是游戏 A 还是游戏 B,本金最后都是减少。在这种不利的条件下,帕隆多教授究竟想出什么策略可以扭转局势呢?
令人惊讶的是,他的思路非常简单:“将游戏 A、游戏 B 组合,50% 的概率进行游戏 A,50% 概率进行游戏 B。”也就是说,游戏 A和游戏 B 分别以 50% 交替进行。帕隆多教授认为,只要将游戏如此组合设计,就有可能使本金呈现增加的趋势。
按照帕隆多教授的思路,下一轮进行哪一个游戏,是由概率决定的。这个概率分别设计为 50%,这就意味着增加游戏次数的情况下,基本都不会出现连续进行游戏 A 或游戏 B 的情况。我们可以再用计算机程序进行 400 次模拟,其中游戏 A 进行 200 次,游戏 B 同样也是 200 次。
不过,原本输多赢少的游戏 A、游戏 B,以 50% 的概率交替进行,就可以让本金增加吗?怎么想都觉得不太靠谱。
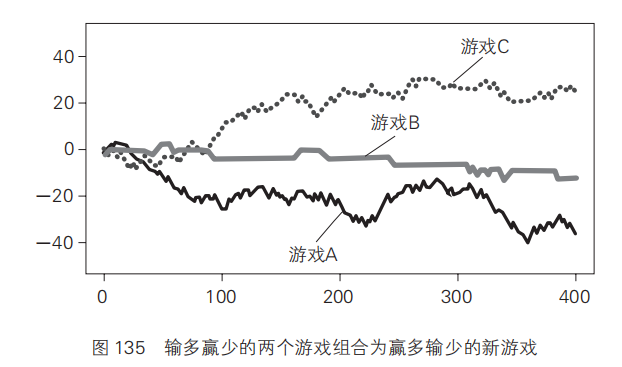
我们马上用计算机程序模拟来看一看结果。将游戏 A 与游戏 B 以 50% 的概率交替进行的形式组合为游戏 C,模拟运行 400 后,就得到了图 135 的结果。为了与游戏 A、游戏 B 对比,图中也加入了单独运行游戏 A、游戏 B 时的结果。
图 135 中,最上方的曲线就是游戏 C 的模拟结果。游戏 C 是游戏 A 和 B 的组合,但是游戏 C 的本金变化趋势却与 A 和 B 截然不同。游戏 C 中的本金是上涨的,而且不是增加一点点儿,是呈现出了整体增加的趋势。
仅仅是让游戏 A、B 交替进行,就导致了颠覆性的结果。这究竟是什么原理?
我们先来用图 134 确认一下游戏的情况。但是图 134 的树状图,只用来说明“进行游戏 A、游戏 B 的结果如何”。并不能解释组合 A和 B 后的颠覆性结果。这是因为,由游戏 A、游戏 B 组合而成的游戏 C 是“动态”的。
因此,随着游戏次数的增多,我们需要考虑游戏 C 中“趋于固定的结果”(这种状态称为稳定状态)。
图 136 呈现了游戏 A、B、C 各自的变化。这个状态图中涵盖了游戏 A、B、C 所有可能的状态,即本金除以 3 后余数为 0、1、2 的情况,以及胜负概率、游戏如何继续的情况。
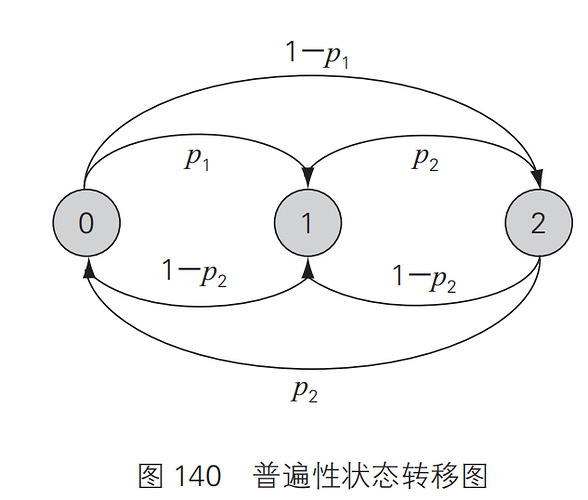
下面我来具体说明一下这个状态转移图的解读方法。因游戏 A、 B 的图的构成机制是相同的,所以这里只选取运行机制更为复杂的游戏 B 进行说明。
在游戏 B 中,当本金除以 3 的余数为 0 时,游戏的胜率只有1%。若游戏获胜,则本金增加 1 元,增加后的本金除以 3 的余数变为 1。这就是图中 0 和 1 之间标有 1% 箭头代表的意思。
当本金除以 3 余数为 2 时,此时本金不能被 3 整除,所以胜率变为 85%,如果获胜,则本金增加 1 元,增加后的本金除以 3 的余数又变为 0。这就是图中 2 和 0 之间标有 85% 箭头代表的意思。
以上分析中选取的都是 1%、85% 的获胜概率,输掉的情况原理也是同样的。类似这样,当前状态在概率的影响下变为下一种状态,这种情况在概率论中称为“马尔可夫链”。
将游戏 A、B 的状态变化的概率相加,然后除以 2,就可以制作出游戏 C 的状态转移图。
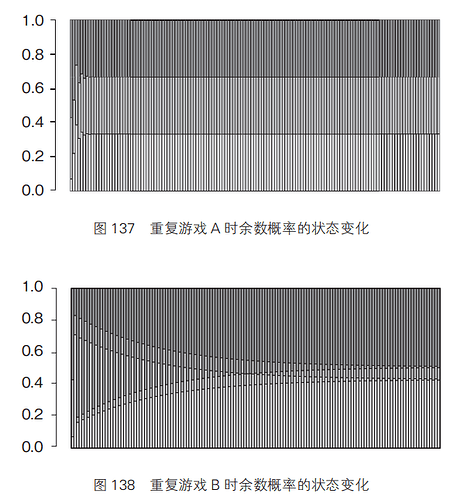
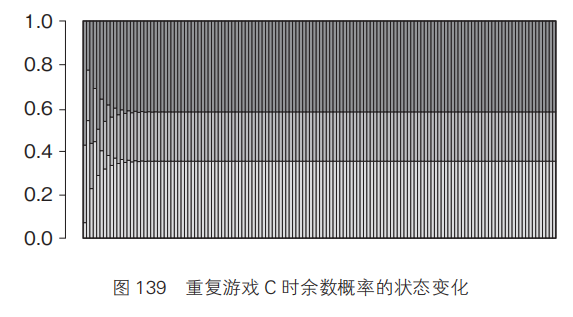
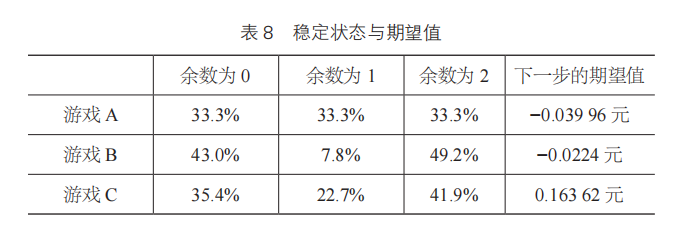
这种状态转移图表示的是进行一次游戏时的状态变化,当游戏次数增加时,余数分别为 0、1、2 的概率又会有什么变化呢?将 0、1、2 比例为 1∶5∶8 的游戏进行 200 次,其变化情况如图 137 ~图 139 所示。
这里需要说明一下,初始状态中把余数为 0、1、2 的比例设置为 1∶5∶8,并没有什么特殊的含义。初始状态选择差异较为明显的比例,会使后续的变化更清晰可见。初始状态设定为其他比例也是完全可以的。
观察图 137 ~图 139 的变化可知,在三个模拟测试中,虽然最初三者的比例有所波动,但最后都分别稳定在了一个固定的比例上。
获胜的原因
图 137 ~图 139 中赌局 A、B、C 各自的状态变化有一个共同规律,那就是本金除以 3 的余数为 0、1、2 的情况,都是分别逐渐趋向一个固定比例。我们可以用表 8 来总结一下这个固定比例。
可 以 看 到, 在 游 戏 A 中, 余 数 为 0、1、2 的概率都同样是33.3%(1/3)。而游戏 B 中,余数为 0 的概率是 43.0% ;余数为 1 的概率是 7.8% ;余数为 2 的概率是 49.2%。在游戏 C 中,三者分别为35.4%、22.7%、41.9%,已经非常接近了(稳定状态)。
这里正是关键所在!请注意,游戏 C 的稳定状态下,三者的比例并不等于 A 和 B 相应数值相加后除以 2 的值。
要判断游戏的条件是有利还是不利,还需要计算出游戏进入稳定状态后的期望值。计算结果显示,游戏 A、B 的期望值均为负数,而游戏 C 的期望值是正的。如图 140 所示,对于游戏 A、B、C 中的任意一个游戏而言,将本金为 3 的倍数时胜率设为 p1 ,不是 3 的倍数时胜率设为 p2 ,只要将 p1 、 p2 设置为特定的一组值,就可以在游戏中获胜。
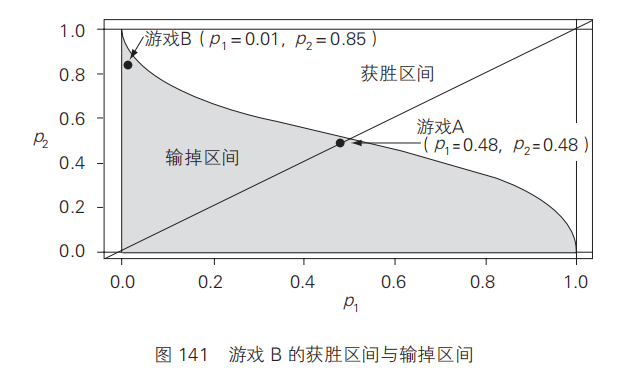
计算 p1 、 p2 各自概率所对应的期望值。将期望值为正的区间(获胜的区间)与期望值为负的区间(输掉的区间)用颜色加以区分,就可以得到图 141。图中上方(白色区域)为获胜区间,下方(灰色区域)为输掉的区间。通过判断 p1、 p2 组合的值落入上方区域,还是到了下方区域,游戏的胜负情况也就一目了然了。
如图 141 所示,游戏 A 的结果为 p p 1 2 = = 0.48(48%),同样游戏 B 中 p1 = 0.01(1%)、 p2 = 0.85(85%),图中这两个游戏的对应的小黑点均位于输掉游戏的区间。
而游戏 C,即将游戏 A 和游戏 B“以特定的比例组合在一起”时,相应的 p1 、 p2 值的组合也应当位于连接这两点的线段上。
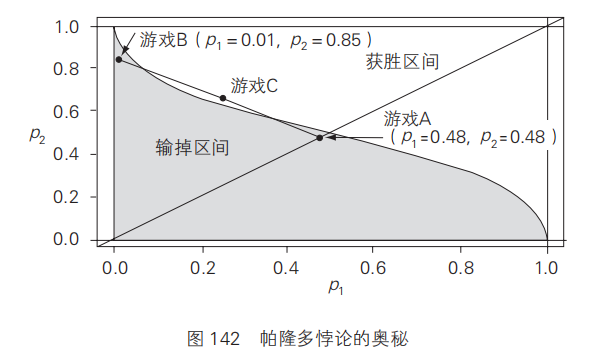
游戏 C 由游戏 A、游戏 B 分别以 50% 的概率组合而成,因此游戏 C p1、 p2 的位置如图 142 所示,为连接游戏 A 和游戏 B 线段的中点。
很明显,代表游戏 C 的点落在了白色获胜区间内。可见,将两个输多赢少的游戏组合起来,确实可以得到一个赢多输少的游戏。实际上,这个意外的反转,是由图中游戏 B 灰色区域的凹陷部分导致的。这也正是帕隆多悖论的奥秘所在。
自帕隆多悖论被提出之后,陆续有一些其他的案例被证明适用于该理论,这些案例都是通过将条件不利的游戏进行组合从而构造出条件有利的游戏。看上去条件不利的游戏,其中其实也隐藏着意外的反转之道。
《数学思考法:解析直觉与谎言》
作者: [日]神永正博
译者:孙庆媛
《简单微积分》作者神永正博经典著作!
分析信息真正价值 / 拆解转化复杂问题 / 破除思维定式陷阱。
通过用数学思维解析实际生活案例、公众认知中的错误直觉、数学经典名题等方式,由浅入深地传授了分析数据信息价值、辨别谎言、拆解转化复杂问题、抓住事物本质的思考之法,同时讲解了相关的数学知识与理论,可以有效提高理性思维、判断与解决问题能力。
《可变思考:数学与创造性思维》
作者:[日]广中平祐
译者:佟凡
日本数学大家、菲尔兹奖得主广中平祐著作!稻盛和夫力荐,呈现数学家观察事物的独特视角与思考方式。
1.稻盛和夫力荐,日本累计销售10万册!
2.菲尔兹奖得主理解“复杂”与“变化”的巧妙视角,用数学的智慧探索创造力的本质
3.讲述创造性思维的本质与根源传授学习、研究、教育中的创造性思维的模式与方法