钱学森曾言“人再笨还能学不会微积分吗？”本文探讨了如何让微积分学习更易懂，介绍了以多维教学、实践应用为特色的《斯图尔特微积分》。
原文标题：钱学森：人再笨，还能学不会微积分吗？
原文作者：图灵编辑部
冷月清谈：
这本教材的核心教学理念是帮助学生发现微积分的实用价值和惊人之美，强调对概念的深入理解。《斯图尔特微积分》通过图像、数值、代数公式和语言描述等多维度方式呈现基本概念，并阐明它们之间的紧密联系，极大地促进了学生的理解。它摒弃了传统的“填鸭式”教学，鼓励学生主动探索发现。
教材的诸多特色板块，如“概念的练习”强化基础理解，“分级的练习”循序渐进提升难度，“现实世界的数据”将抽象概念与实际应用相结合，让学习不再枯燥。“专题项目”则提供了应用、探索和写作等多种扩展学习路径，培养学生解决问题的能力与成就感。此外，它还系统介绍了乔治·波利亚的“解题的基本原则”，并引导学生合理利用技术工具，如绘图软件、图像计算器等，以可视化和计算辅助学习。《斯图尔特微积分》的出版旨在为教师和学生提供个性化学习微积分的工具，使这门“难学”的学科变得触手可及，适合不同学习风格的人群。
怜星夜思：
2、文章提到微积分有实用价值和惊人之美，它不仅是工程学基础。大家在生活或者其他学科里，还见过哪些“悄悄”应用了微积分的例子？说不定能颠覆我们的认知！
3、《斯图尔特微积分》强调概念理解、可视化和现实数据，已经很先进了。抛开教材本身，大家觉得未来微积分教学还能怎么玩，才能更“接地气”，让更多人觉得学起来不那么头大？
原文内容
28岁时，钱学森与导师冯·卡门共同提出了"卡门-钱近似"公式，解决了高速空气动力学难题。
35岁，开创了物理力学学科。
43岁，出版了《工程控制论》，创立“用不可靠元件组成可靠系统”的理论，奠定现代控制论基础。
回国后在火箭导弹技术、航天事业、农业、林业乃至社会经济各个领域均有重要贡献。
他还认为一个人的智力巅峰是20岁，这个时候出科研成果是最容易的，按这个年龄进行倒推的话，孩子们应该4岁入学，8岁小学毕业，16岁之前大学毕业，18岁硕士毕业开始报效祖国。
按钱老的安排，12岁就要开始学微积分了！怕不是还真有点难了。
但《斯图尔特微积分》还真的做到了人性化！至少聪明一些的初中孩子已经可以入门学习了，而高中孩子完全可以无障碍学习。读者评价其为“立体化的微积分教材”“内容由浅入深、循序渐进的独门秘籍”“高级的人性化教学”。
《斯图尔特微积分（上）》
作者：[加] 詹姆斯·斯图尔特
译者：程晓亮、徐宝、华志强
01
什么是好的微积分教学？
马克·范·多伦（Mark Van Doren）说，教学是帮助学生发现的艺术．《斯图尔特微积分》这一版延续了之前版本的传统，我们希望帮助学生发现微积分的实用价值和惊人之美．我们的目的是向学生展现微积分的实用性，并促进学生技术能力的发展，同时让学生学会欣赏微积分的内在美．
牛顿在做出这个重大发现时无疑会有一种胜利感，希望学生也能体验到这样的感觉．
微积分学习的重点在于理解概念．几乎所有教授微积分课程的教师都认为理解概念应该是微积分教学的最终目标．
为实现这一目标，我们将以图像、数值、代数公式和语言描述等方式呈现基本概念，并强调这些不同的表示方法之间的关系．
可视化、数值和图像实验以及语言描述可以极大地促进学生对概念的理解．此外，理解概念和掌握技能可以齐头并进，相互强化．
我们清楚地意识到，好的教学有不同的形式，微积分的教与学也有不同的方法，所以我们设计的讲解和练习考虑到了教与学的不同风格．
本书的特色板块（包括专题项目、扩展练习、解题的基本原则和历史见解）强化了基本概念的学习和核心技能的掌握．我们的目标是为教师及学生规划他们自己的微积分发现之路提供所需的工具．
每个特色板块都是补充不同的教学实践的材料．贯穿全书的有历史见解、扩展练习、专题项目、解题的基本原则，以及许多使用技术工具根据概念进行实验的机会．
我们知道，在一个学期中很难有足够的时间来让所有的特色板块发挥作用，不过教师可以有选择性地使用，以吸引学生的注意力，进而强调微积分的丰富思想及其在现实世界中的重要意义．
02
特色板块
概念的练习
培养概念理解能力最重要的方法是解决教师布置的问题．为此，本书囊括了各种类型的问题．一些练习开始时要求读者解释该节中出现的基本概念的含义（例如，2.2节、2.5节、11.2节、14.2节和14.3节前几个练习），大多数练习是为了强化读者对基本概念的理解（例如，2.5节练习3~10，5.5节练习1~8，6.1节练习1~4，7.3 节练习1~4，9.1节练习1~5，11.4节练习3~6）．其他练习通过图像或表格检验读者对概念的理解（例如，2.7节练习17，2.8节练习36~38和练习47~52）．许多练习都用图像将问题可视化（例如，6.2节练习1~4，10.4节练习43~46）．还有一些练习使用语言描述来检验读者对概念的理解（例如，2.5节练习12，2.8节练习66）．此外，所有复习小节都以概念题和判断题开始．我们特别重视图像、数值和代数方法的结合和比较（例如，2.6节练习45~46，3.7 节练习29，9.4节练习4）
分级的练习
每节的练习都经过仔细的分级，从有关基本概念的练习，到训练技巧和绘制图像的练习，再到更具挑战性的练习，它们通常扩展了该节中的概念，回顾了前几节中的概念，或者涉及应用和证明．
现实世界的数据
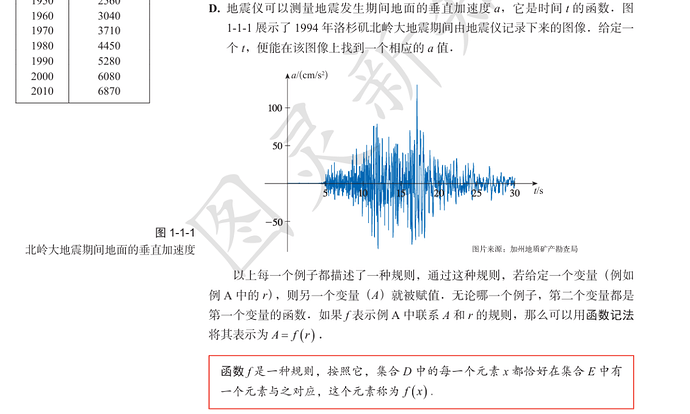
现实世界的数据为介绍、引入或说明微积分的概念提供了切实可行的方式．因此，许多例题和练习所处理的函数都是由这些数据或其图像定义的．这些现实世界的数据来自相关公司和政府机构，以及互联网和图书馆．例如，1.1节图1-1-1（北岭大地震的地震图），2.8节练习36（整容手术的数据），5.1节练习12（“奋进号”宇宙飞船的速度），5.4节练习83（新英格兰地区各州的耗电功率）， 14.4节例3（热指数），14.6节图14-6-1（温度的等值线图），15.1节例9（科罗拉多州的降雪量），以及16.1节图16-1-1（旧金山湾区的风速向量场）
专题项目
令学生积极投入学习的途径之一是引导他们（可以采用小组形式）参与扩展专题，完成专题项目可以给学生一种巨大的成就感．
本书中有三种专题项目．
应用专题包括能激发学生想象力的应用题．9.5节末的专题研究被向上抛的球到达最高点和回到原高度，哪个所用的时间更长（答案可能会让你惊讶）． 14.8节末的专题用拉格朗日乘数法来确定三级火箭的每一级的质量，使得火箭以最小的总质量达到所期望的速度．
探索专题提出将在之后讨论的结论，或者通过识别规律来引导发现（例如，7.6 节末的专题探讨积分的规律）．一些探索专题研究几何方面的问题：四面体（12.4节末）、超球体（15.6节末）和三个圆柱体的交（15.7节末）．此外，12.2 节末的专题使用导数的几何定义来求悬链线的公式．一些专题充分利用了技术工具：10.2节末的专题展示了如何使用贝塞尔曲线设计字母的形状用于激光打印机．
写作专题要求学生将今天的方法与微积分奠基人所用的方法进行比较，例如，2.7节末的专题中费马求切线的方法．另外，写作专题中还提供了参考文献．
解题
学生通常很难解决不能通过明确的步骤得到答案的问题．作为乔治·波利亚的学生，詹姆斯·斯图尔特最先了解到波利亚对解题过程的令人愉快且精辟的见解．在第1章末的“解题的基本原则”中，斯图尔特对波利亚的四步解题法做了改进．这些原则在整本书中都有明确和隐含的应用．其余每一章后面都有一个叫作“附加题”的小节，提供了解决具有挑战性的微积分问题的例子．在解决“附加题”中的问题时，要牢记大卫·希尔伯特（David Hilbert）的建议：“ 为了吸引我们，一道数学题应该是困难的，但也不能是难以触及的，以免辜负我们的努力．”我们在自己的微积分课上，用这些问题获得了很好的效果．看到学生们如何应对挑战是令人欣慰的．詹姆斯·斯图尔特说：“当我把这些具有挑战性的问题放到作业和测试中时，我会用不同的方式打分……如果学生能提出解题思路并识别出与问题相关的解题原则，我就会给他们加分．”
技术工具
使用技术工具时，清楚地理解屏幕上的图像或计算结果背后的概念尤为重要．如果使用得当，那么图像计算器和计算机是发现和理解这些概念的有力工具．本书既可以在有技术工具的情况下使用，也可以在没有技术工具的情况下使用．我们使用两个特殊标记来表示何时需要技术工具提供特定的帮助．图标
表示练习需要使用绘图软件或图像计算器来帮助完成作图．（这并不是说作图技术不能用于其他练习．）图标
表示练习需要借助软件或图像计算器，而不是仅仅通过作图就能完成．WolframAlpha和Symbolab等免费网站通常是适用的．如果需要计算机代数系统的全部资源，比如Maple或Mathematica，则会在练习中说明．当然，技术工具不会让笔和纸过时．动手计算和画图通常比使用技术工具更有利于说明和强化一些概念．教师和学生都需要培养判断能力，知道何时适合使用技术工具，何时通过动手计算会获得更多的领悟．
《斯图尔特微积分（上）》
作者：[加]詹姆斯·斯图尔特(James Stewart)
[美]丹尼尔·克莱格(Daniel Clegg)
[美]萨利姆·沃森(Saleem Watson)
译者：程晓亮 徐宝 华志强
长销40年，影响全球超800万学生的经典！全彩印刷，版式精美，100%还原英文原书
1.传世的杰作、教科书的典范，传奇数学家斯图尔特最具代表性的著作首次全新中文版上市！
2.长销40年，影响全球超800万学生，哈佛、加州伯克利、哥大等顶尖学府指定教材；
3.轻松入门微积分，一站直通高等数学：从中学到大学毕业，全阶段适用，完美衔接初等数学和高等数学，完整搭建微积分知识体系；
4.引导式教学，立体化讲解，再也不被传统教材的“防自学设计”所困扰！
5.先直观认识，后严格定义，拒绝“填鸭式”学习，贴近生活的现实案例和跨学科应用，培养数学思维，提高解题能力。