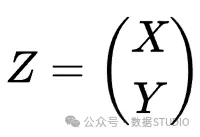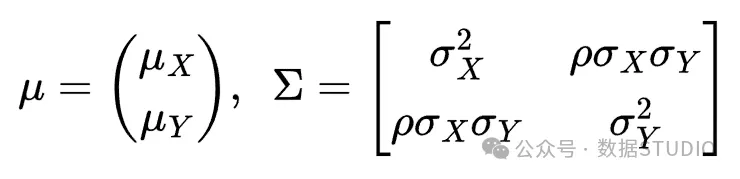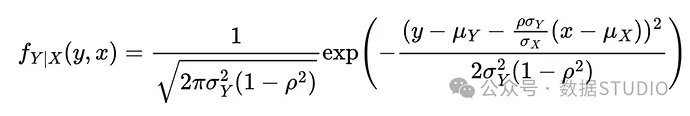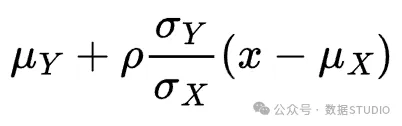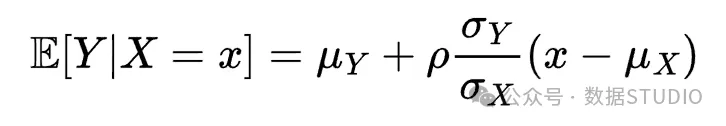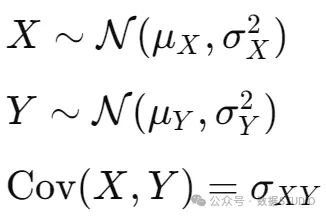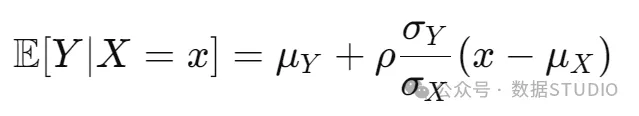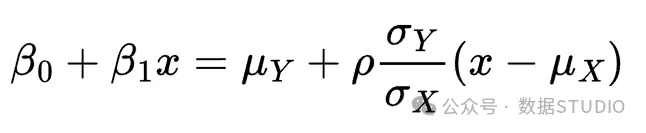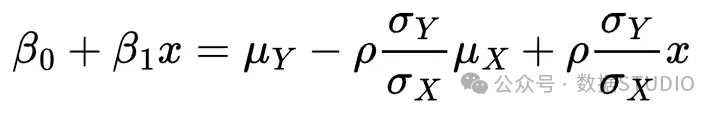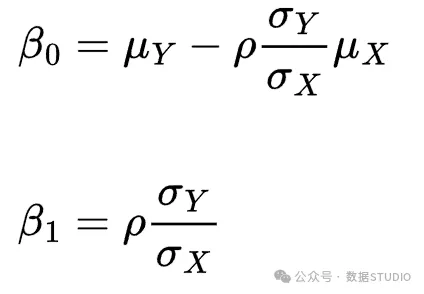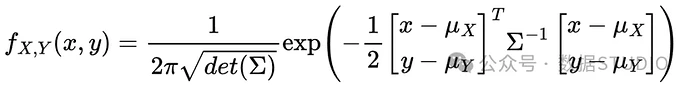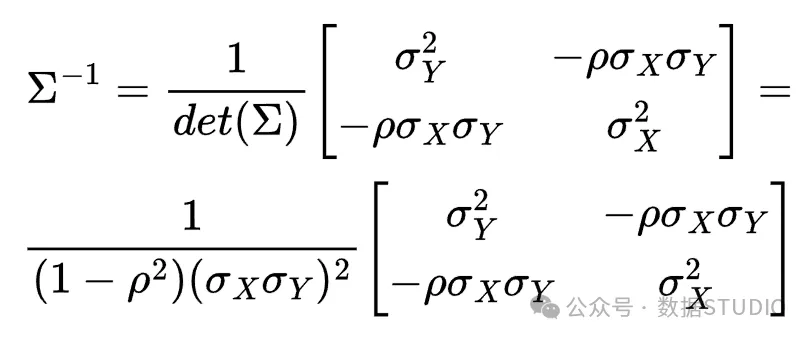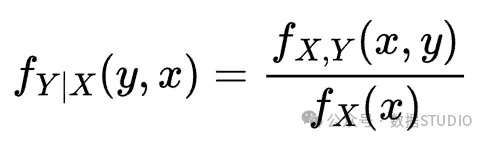二元正态投影,预测变量间关系、赋能线性回归与异常检测。
原文标题:统计学必知:二元正态投影
原文作者:数据派THU
冷月清谈:
怜星夜思:
2、文章里提到了二元正态分布,那要是我们的数据不符合正态分布,或者干脆是离散数据,是不是二元正态投影就没法用了?有没有类似的替代方法或者怎么处理这种非正态数据呢?
3、看到文章里那些3D图和散点图,以及它解释说相关系数rho会怎么影响分布形状。有没有什么更形象的比喻或者小技巧,能帮我们快速理解这种“投影”带来的预测能力和方差变化?感觉纯看公式还是有点抽象。
原文内容

本文约2200字,建议阅读5分钟双变量投影有助于在给定一个随机变量的特定值的情况下,确定另一个随机变量的预期值。
在统计学和机器学习中,理解变量之间的关系对于构建预测模型和分析数据至关重要。探索这些关系的基本技术之一是双变量投影(二元投影),它依赖于双变量正态分布的概念。该技术利用变量之间的依赖结构,可以检查和预测一个变量相对于另一个变量的行为。
双变量投影有助于在给定一个随机变量的特定值的情况下,确定另一个随机变量的预期值。例如,在线性回归中,投影有助于估计因变量相对于自变量的变化情况。
本文分为三部分:
-
第一部分,我将探讨二元投影的基础知识,推导其公式并演示其在回归模型中的应用。
-
第二部分,我将提供一些投影背后的直观解释,并绘制一些图表以便更好地理解其含义。
-
第三部分,我将使用该投影推导线性回归的参数。
在推导二元投影公式时,我将运用一些通用知识。为了避免给读者带来理解困惑,我将在文章末尾的附录中提供这些论述的证明和参考文献。有不明白的地方可以查看原文章。
第一部分:二元正态投影公式
令 为服从正态二元分布的随机向量 ,其中
Z 的形式,其中 X 和 Y 随机变量服从正态单变量分布Z的形式,其中 X 和 Y 随机变量服从正态单变量分布
以 X 和 Y 的均值和方差表示 Z 的均值和协方差矩阵。ρ 是 X 和 Y 之间的相关性。以 和 的均值和方差表示 的均值和协方差矩阵。 是 和 之间的相关性。
然后,给定 , 的条件分布是正态的,并且由下式给出:
你可以在文章末尾的附录中找到该结果的推导
这是具有条件均值的正态分布的密度
和条件方差
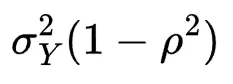
现在我们可以写出 在 上的线性投影,即给定 时 的条件平均值:
这是 和 之间的线性关系,因为它是 在 上的线性投影。
这个公式告诉我们什么?在实际应用中我们能用到什么?让我们来一探究竟!
第二部分:解释和模拟
双变量投影在预测模型中起着至关重要的作用,它使我们能够根据一个变量的值来估计另一个变量的预期值。我将使用线性回归来举一个实际的例子。
除了其预测能力之外,双变量投影还能提供关于两个变量之间关系的性质和强度的宝贵见解。例如,我将在另一篇文章中运用这一结果,探讨试图控制订单流的做市商的凯尔模型。在该模型中,做市商试图了解给定订单流的证券预期价值。
机器学习的另一个应用是检测异常值或离群值。通过投影,这个过程变得更加易于管理,因为它可以突出显示变量之间与预期关系的偏差。
在使用线性回归进行实际示例之前,我将运行一些 Python 模拟,以更好地突出二元正态分布的形式及其投影的预期结果。
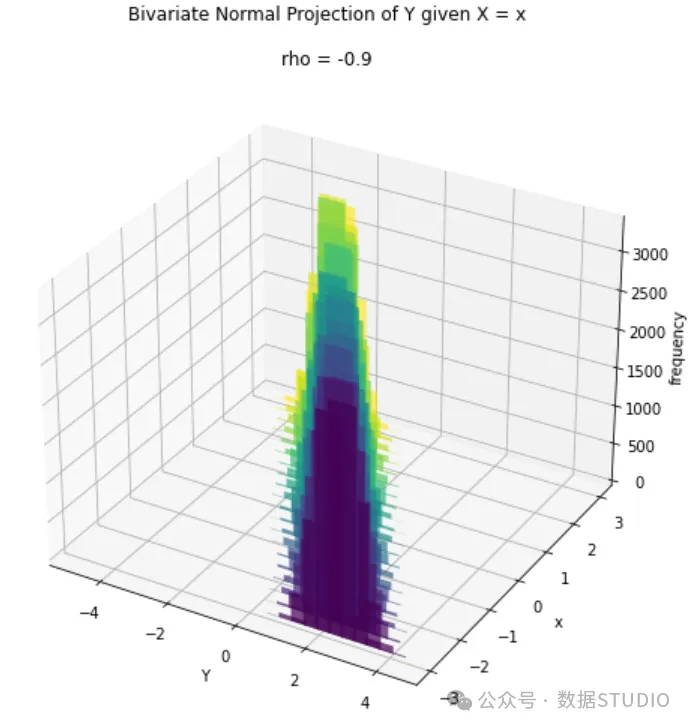
在下图中,随机变量 和 服从标准正态分布 。我们将看到,当设置不同的相关系数 值时,图形会如何变化。
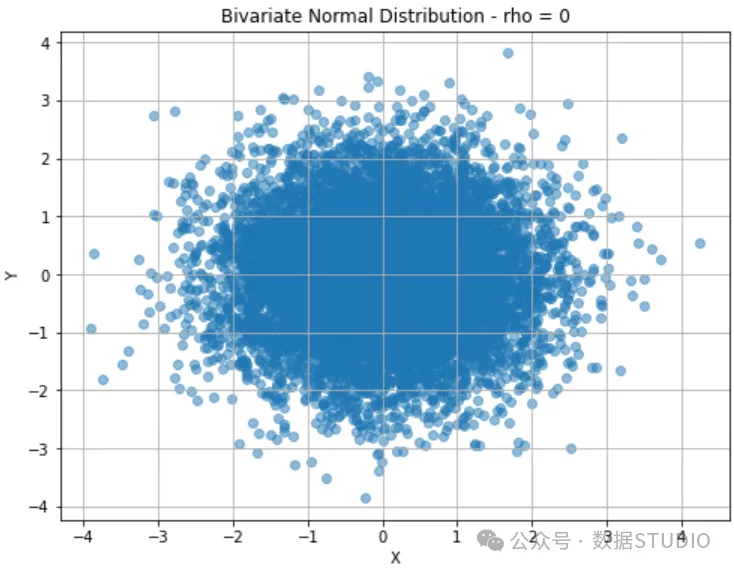
第一个边缘情况可能是设置 ,这意味着两个随机变量不相关:
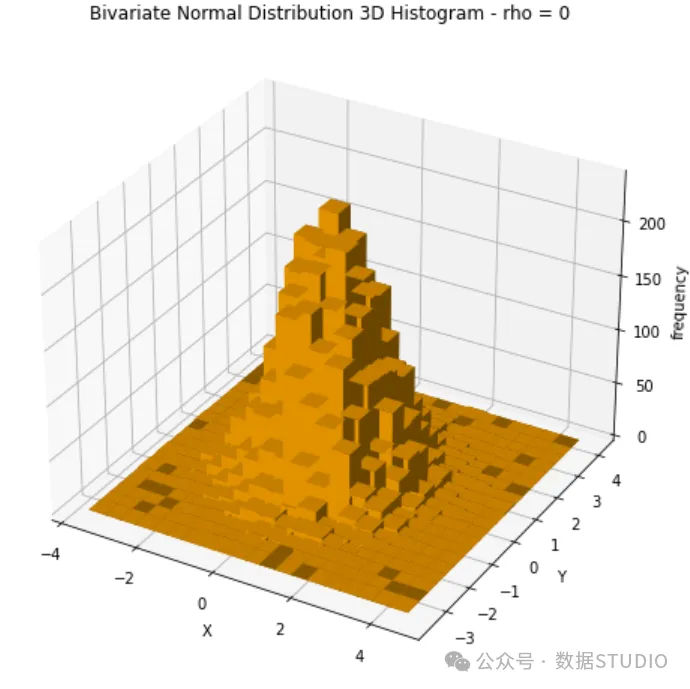
这里,两个随机变量以它们的均值0为中心,散点图呈圆形。这表明变量是独立的。变量之间没有明显的线性关系。在下面的 3D 图中,你可以更好地理解分布的形式。
现在让我们应用投影公式,看看当 的不同值时Y的分布会发生什么变化。
可以想象, 的分布不会受到 不同值的影响。Y的平均值及其方差保持不变。
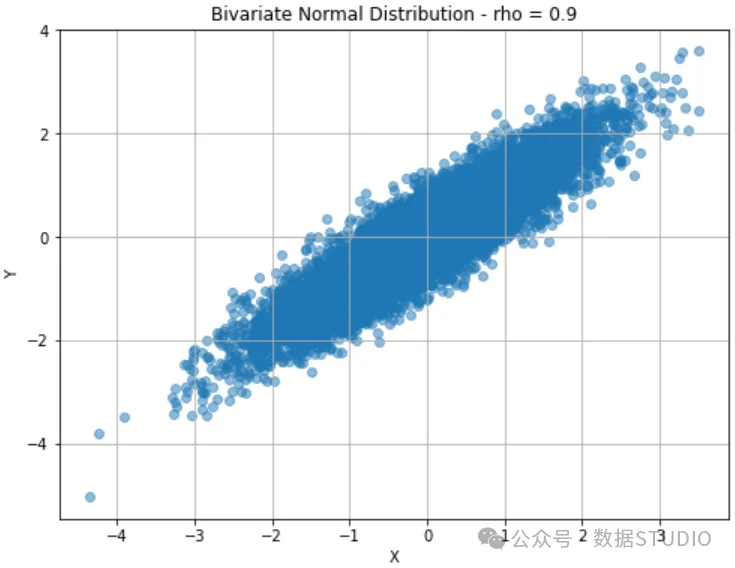
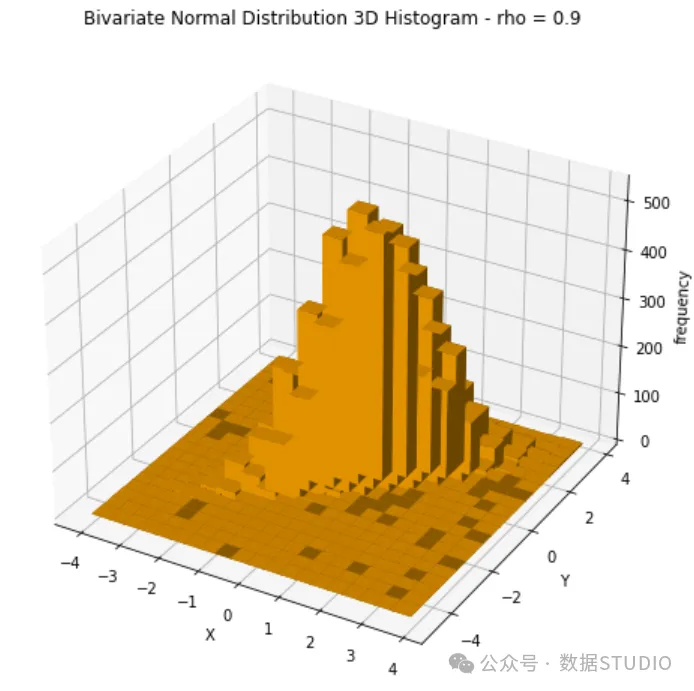
现在我们看看更有意义的相关性会发生什么。设 :
两个变量的平均值仍然以0为中心,但散点图显示出明显的线性关系。3D 图如下所示,你可以看到,现在的分布不再像上一个示例那样呈现“锥体”形状。
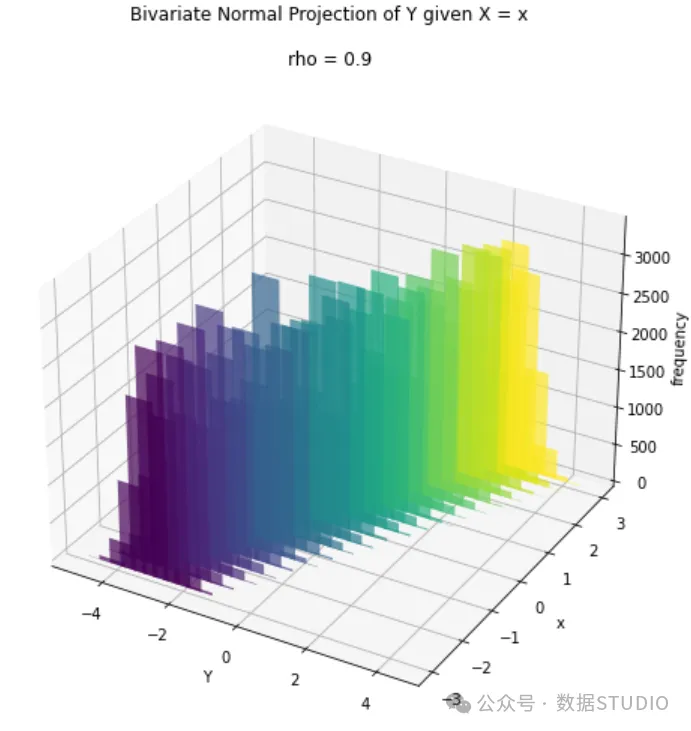
绘制投影图后,我们可以看到Y的分布实际上受到不同 值的影响。有趣的是, 的平均值依赖于 (因为它的值取决于 与 X之间的差值),而 的方差不随 变化,因为它仅依赖于相关性 ρ 。此外,注意到方差小于 ρ=0 的情况,因为它与1-ρ² 成比例。
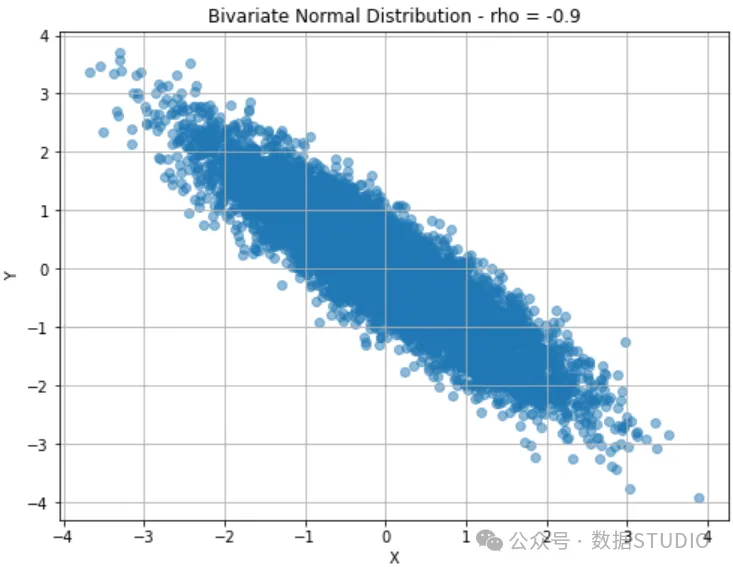
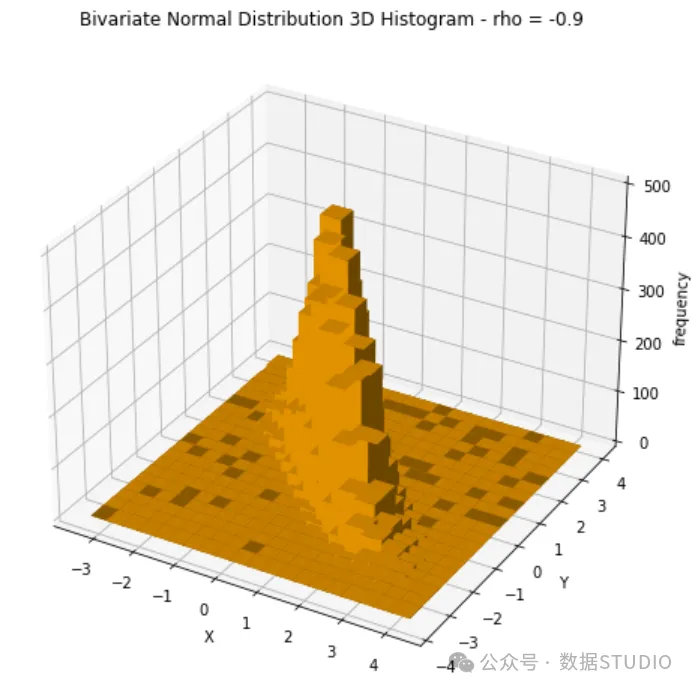
我将展示的最后一个案例是ρ 。注释与上一个案例非常相似:
第 3 部分:应用--线性回归
现在让我们将投影应用到一个简单的机器学习案例:线性回归。假设我们要构建一个机器学习模型,使用房屋表面的值( 变量)来预测房屋价格( 变量)。我们有一个包含 和 历史数据的数据集。
假设变量分布如下,并且它们具有线性关系:
我们希望建立一个模型,在给定 的某个特定值的情况下,能够预测Y的值:
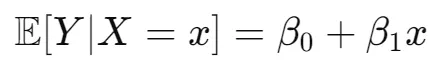
其中 表示线性回归的系数,与通常情况一样:
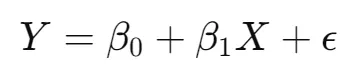
使用投影公式,我们有
这样,我们可以使用(从数据集估计的)分布参数来估计线性回归系数。首先使两个表达式相等:
重新排列右边的项,将与 相乘的项和不与 相乘的项分开:
为了使方程成立,参数应该是:
注意,这些是线性回归参数的估计量!
写在后面
线性投影是统计学中一个强大的工具。它应用广泛,你可能会惊讶于它被非显式地使用了多少次。
附录——二元线性投影推导
首先定义两个随机变量 和 的连接密度函数:
计算协方差矩阵的行列式:
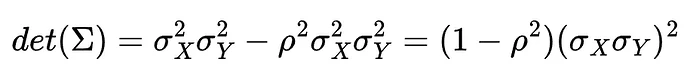
以及协方差矩阵的逆:
将其代入密度函数表达式中,我们得到:
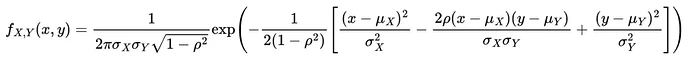
现在,正态二变量的边际概率密度函数是正态单变量。 的边际函数由以下公式给出:
参考:https://en.wikipedia.org/wiki/Marginal_distribution现在我们终于可以计算给定 的 的条件分布了。注意,这仍然是正态分布:
参考:https://en.wikipedia.org/wiki/Conditional_probability_distribution代入联合密度函数和边缘密度函数,我们得到投影密度
投影公式现在是给定 时 的期望值,可以通过对投影密度函数进行积分计算得出。注意,指数函数中的二次项可以解释为随机变量减去其均值。在这种情况下,均值是 乘以依赖于 的项。我们在绘制分布图时就注意到了这种效果。方差按 ρ ² 缩放。
分布的预期值为
这就是双变量投影。