中科大提出基于可微分隐藏状态(DHS)的神经ODE框架,用以解决不规则时间序列问题。通过注意力机制和Hoyer度量,优化动态建模,实验证明有效。
原文标题:ICDE 2025 | 神经常微分方程在不规则时间序列中的应用
原文作者:数据派THU
冷月清谈:
怜星夜思:
2、文章中提到Hoyer度量用于提高时间关系建模的精度,为什么要最大化Hoyer度量?Hoyer度量在时间序列分析中还有哪些应用场景?
3、文章在多个数据集上验证了DHS模型的有效性,你认为DHS模型在哪些实际应用场景中最有潜力?为什么?
原文内容
本文介绍一篇 ICDE 2025 中的关于神经常微分方程(NODE)在不规则时间序列分析中的应用研究。来自中科大的研究者们提出了一种基于可微分隐藏状态(DHS)的增强型神经 ODE 框架。通过引入注意力机制和 Hoyer 度量来优化时间序列的动态建模,并在多个数据集上验证了模型的有效性。
【论文标题】
Neural ODE with Differentiable Hidden State for Irregular Time Series
【论文地址】
https://www.computer.org/csdl/proceedings-article/icde/2025/360300c107/26FZAEab0hq
论文背景
不规则时间序列数据在各种现实世界应用中无处不在,包括疾病预防、金融决策和地震预测等。不规则时间序列数据的特征是非均匀采样,观测值在不同时间间隔发生。这种不规则性,加上由于技术问题或数据质量问题导致的频繁缺失数据,给现有的时间序列分析方法带来了挑战,包括基于RNN的模型和Transformer变体。
NODE 由于其顺序处理能力和处理不规则采样数据的能力,已成为不规则时间序列建模的热门且有前景的方法。通过使用适当的常微分方程(ODE)来建模不规则时间序列的动态,可以通过对 ODE 进行积分,从不规则采样的数据中重建连续且完整的时间序列。
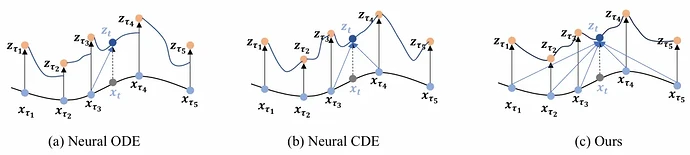
然而,基于 NODE 的方法在不规则时间序列建模中面临一个基本挑战。它们从初始值开始积分以推导出所有后续值,而没有考虑初始点之后的观测数据点。它们在每个时间点将潜在状态与观测值进行积分,即在不同时间间隔有不同的初始值。尽管这种机制可以达到一定的准确性,但它只考虑每个时间点的一个观测值,忽略了观测值之间的相关性。同时,这种机制导致潜在过程被分割,可能无法准确反映真实的动态过程,如图1(a)所示。
图1:Neural ODE、Neural CDE以及本文方法的示意图
为了解决 NODE 中潜在状态碎片化的问题,神经控制微分方程(NCDE)方法涉及对观测值进行插值以估计潜在过程,例如Kidger等人(2020)中使用的自然三次样条插值。这种估计过程随后引导积分路径,使模型能够纳入后续观测值。尽管这种方法简单,但它未能充分利用数据的全部信息内容。如图1(b)所示,这种方法仅在给定时间点取两个最近的观测值,且使用插值算法无法很好地建模时间序列中的时间相关性。
针对现有解决方案固有的局限性,本文提出了 DHS 增强的神经 ODE 框架,这是一种数据驱动的方法,旨在巧妙地捕捉时间动态,同时确保潜在过程的无缝连续性。引入了基于注意力的微分隐藏状态,将不规则采样的观测值视为将时间序列映射到隐藏状态空间的投影矩阵。由于投影是线性的,隐藏状态保留了原始时间序列的连续性。
所提方法利用广义逆理论,创新性地反向工程注意力机制,得到描述隐藏状态动态的 ODE。为了提高时间关系建模的精度,作者整合了 Hoyer 度量。通过战略性地最大化Hoyer度量,本文框架优化了模型对细微但显著的时间变化的识别能力,从而提高了预测的准确性和可靠性。
论文方法
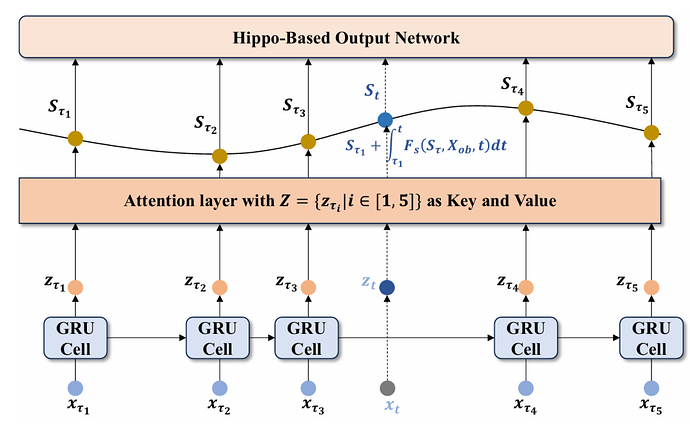
上图展示了模型的整体架构:将不规则采样的观测数据输入神经网络以生成 Z,Z 随后作为注意力层的 key 和 value 用于生成可微隐藏状态。整个框架的输出通过基于 Hippo 架构的输出网络生成。
01、建模时间序列的ODE
作者首先定义了不规则时间序列表示为 ,其中 是在时间点 处的观测值, 是观测时间点的集合。为了建模隐藏状态 的连续动态,作者提出了以下常微分方程(ODE):
其中, 表示隐藏状态的动态。给定任意时间 ,隐藏状态 可以通过对上述 ODE 进行积分获得:
最终,通过一个读出函数 可以从隐藏状态生成时间序列在时间 处的输出:
02、基于离散观测的注意力可微分隐藏状态
为了捕捉时间序列的动态变化,作者提出了可微分隐藏状态(DHS) 。DHS是通过将观测值映射到隐藏状态空间来生成的,具体步骤如下:
-
观测值的嵌入:对于每个时间点 的观测值 ,通过一个神经网络 将其映射到隐含表示 :
其中, 表示 的历史观测值。
-
注意力机制:将所有观测时间点的隐含表示 作为"键"(Key)和"值"(Value),将当前时间点的隐含表示 作为"查询"(Query),通过注意力机制生成DHS:
其中, 是注意力分数, 是归一化的注意力分数, 是DHS。
03、DHS的导数
为了将 DHS 的动态建模为 ODE,作者计算了 DHS 关于时间 的导数。根据链式法则,DHS 的导数可以表示为:
其中, 是将 转换为对角矩阵。由于 无法直接计算,作者引入了一个新的神经网络 来建模:
因此,DHS 的导数可以表示为:
为了将注意力分数 和隐含表示 表示为DHS 的函数,作者利用了广义逆理论。通过求解线性方程组,得到了 和 的表达式,并最终得到了描述 DHS 动态的 ODE。
04、输出
DHS 提供了一个连续的隐藏嵌入,可以方便地用于下游任务。对于分类任务,可以直接通过一个简单的神经网络将DHS映射到输出:
对于插值和外推任务,可以在任意时间点 通过对应的 获得输出 。
此外,DHS 还可以与其他方法(如Hippo)结合使用。Hippo 是一种有效的时间序列表示方法,但需要连续序列作为输入,而 DHS 正好提供了这样的输入。作者构建了一个结合 DHS 和 Hippo 的系统方程,进一步增强了模型的性能。
实验结果
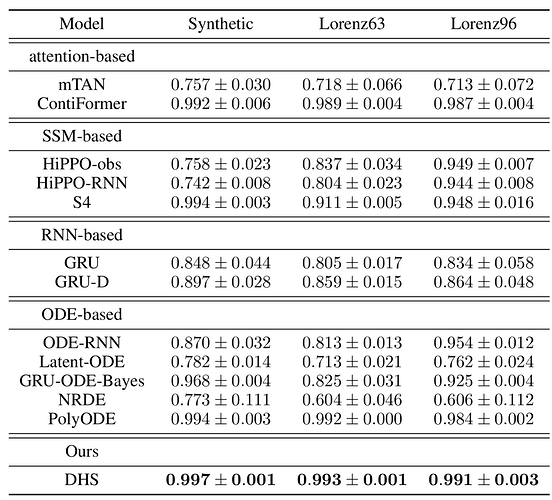
作者在以下四个数据集上进行了实验:合成周期数据集,动态系统,美国历史气候网络,PhysioNet Challenge 2012。将 DHS 模型与以下多种基线方法进行了比较:基于注意力的模型,基于 SSM(State Space Model)的模型,基于 RNN 的模型和基于 ODE 的模型。实验结果如下:
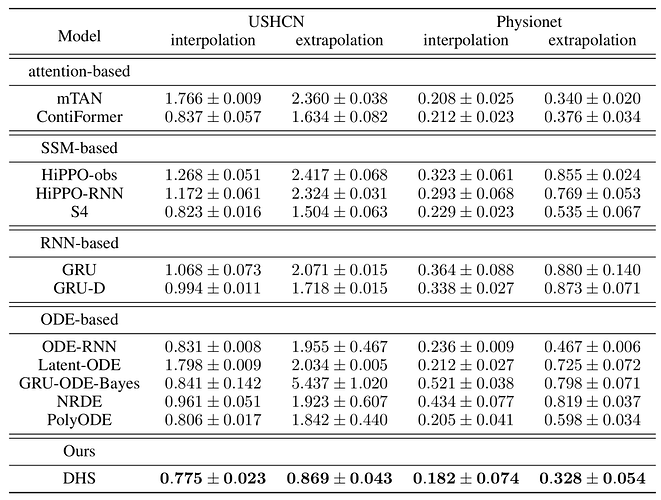
作者使用 USHCN 和 Physionet 数据集评估了模型在插值和外推任务上的性能。结果如下:
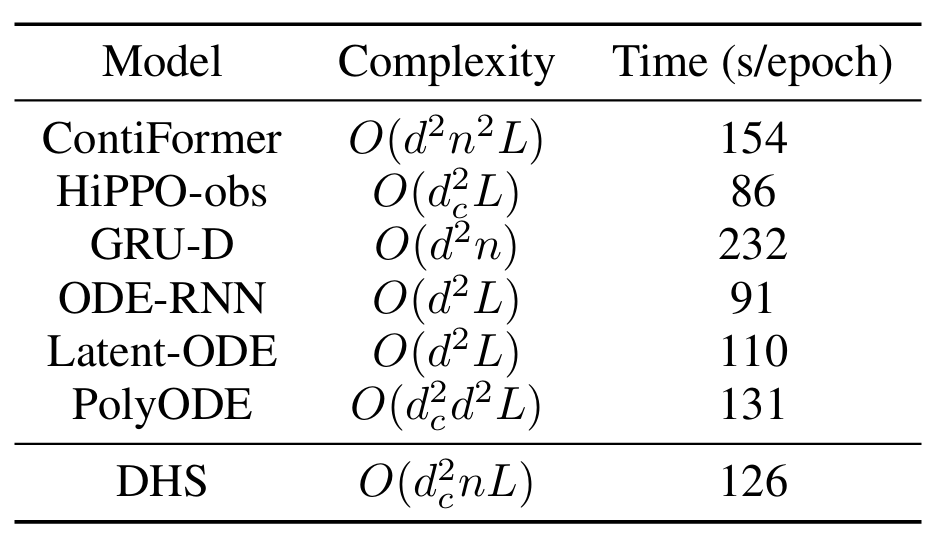
作者比较了 DHS 模型与代表性基线方法的时间复杂度,并列出了在 USHCN 数据集上每个训练周期的时间消耗。结果如下:
通过在多个数据集和任务上的实验,作者证明了 DHS 模型在不规则时间序列分析中的有效性。
DHS 通过引入基于注意力的微分隐藏状态空间,能够更好地捕捉时间序列的动态变化,并在分类、插值和外推任务上均取得了优异的性能。
此外,DHS 模型在时间消耗方面也表现出色,能够在可接受的时间内实现高性能。
总结
本文针对当前神经 ODE 方法面临的一个关键挑战:其在处理不规则时间序列时,难以在保持潜在动态连续性的同时无缝整合上下文信息。为解决这一问题,作者提出了一种基于注意力机制的微分隐状态空间,通过将不规则采样观测值作为键值矩阵来增强模型的上下文感知能力。基于这一创新性隐状态空间,作者运用广义逆理论构建了能够封装隐状态随时间演化的 ODE 方程。为提升时间关系建模的精确度,引入 Hoyer 度量准则,旨在隐状态生成过程中最大化注意力得分的稀疏性。通过合成数据集和真实数据集的系统实验验证,本文的方法在与现有前沿模型的对比中 consistently(始终如一地)展现出更优的不规则时间序列分析效能。