中国科学技术大学团队发布时间序列预测(TSF)综述,全面总结TSF的核心建模范式、关键挑战、方法演化与未来方向,构建出一个系统知识框架。
原文标题:综述 | 一文读懂时间序列预测研究全景:方法、挑战与未来方向
原文作者:数据派THU
冷月清谈:
怜星夜思:
2、文章中提到了时间序列基础模型,类似于NLP领域的BERT,这种基础模型在时间序列领域有哪些潜在的应用场景?会给时间序列分析带来哪些变革?
3、文章提到了可解释的AI对于时间序列预测的重要性,那么,在现有的技术条件下,有哪些方法可以提高时间序列预测模型的可解释性?
原文内容
时间序列预测(Time Series Forecasting, TSF)已成为推动智能化决策的关键能力,广泛应用于金融分析、供应链优化、设备监测、气象预测等领域。在数据体量不断扩大、结构愈发复杂的背景下,如何精准地刻画序列演化趋势、构建高效可信的预测模型,成为学术界与工业界共同关注的核心问题。近日,来自中国科学技术大学的研究团队发布了一篇全面综述性论文,研究围绕 TSF 的核心建模范式、关键挑战、方法演化与未来方向进行全面总结,构建出一个覆盖传统统计建模、深度学习、预处理技术、迁移学习、大模型与可信预测的系统知识框架。
【论文标题】
A Comprehensive Survey of Time Series Forecasting: Concepts, Challenges, and Future Directions
【论文地址】
https://www.techrxiv.org/users/909144/articles/1283131-a-comprehensive-survey-of-time-series-forecasting-concepts-challenges-and-future-directions
【论文仓库】
https://github.com/USTCAGI/Awesome-Papers-Time-Series-Forecasting
🌟 文章亮点概览
-
系统定义 TSF 问题及评价方法
-
深入剖析 TSF 面临的十大挑战
-
多维度多角度的时间序列预处理范式
-
全景式回顾统计模型与数据驱动时序预测方法
-
覆盖迁移学习、大模型、可信预测等前沿方向
一、基础概念与定义:时间序列预测的底层逻辑
1.1 时间序列数据概览
时间序列通常被定义为按时间顺序索引的数据点序列,其中每个观察值是在特定(通常是均匀的)时间间隔内获得的。尽管数据通常在离散的间隔内记录(例如,每小时、每天、每月),但这些观察值所基于的许多实际现象可以被视为连续的,并且原则上在时间和价值上都是无界的。因此,时间序列建模必须同时处理测量的离散性质和过程本身的潜在连续性,并深入建模数据的趋势性、周期性和不规则动态变化。
1.2 时序预测任务概览
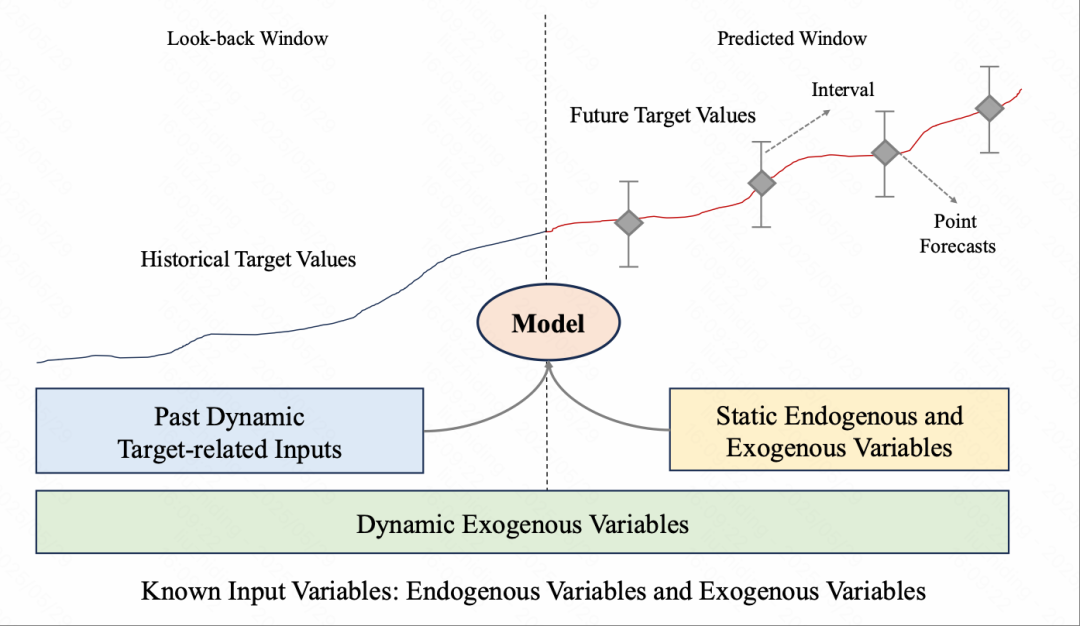
时间序列预测任务旨在基于过去的观察值以及潜在的协变量来预测目标系列的未来值,涉及多个核心概念:
回顾窗口(Look-back Window):指目标时间序列中最近 L 个时间步的连续观测值,作为主要的历史上下文信息来源,用于建模趋势、季节性和其他时间依赖关系。
协变量(Covariates / 外生变量):除目标序列外,许多应用还利用气象、经济或人口等外部因素作为辅助输入。这些变量有助于提升模型对外部驱动因素的建模能力。
预测窗口(Predicted Window):预测任务的输出通常是一段未来时间步,长度可以从单步(如下一小时)到多步(如下一周或下月)不等。
单步 vs 多步预测(One-step vs. Multi-step):单步预测每次仅预测一个未来时间点,适用于逐步滚动预测;多步预测则一次性输出多个未来时间点,能够建模长期依赖,但可能引入更大的误差累积。
单变量 vs 多变量预测(Univariate vs. Multivariate):单变量预测仅依赖目标序列本身;多变量预测则引入多个相关序列或协变量,以挖掘跨序列间的依赖关系,从而提升精度。
迭代 vs 直接预测策略(Iterative vs. Direct Strategies):迭代策略逐步生成未来值,并将其作为输入用于后续预测;直接策略则为每个未来时间步构建独立的预测机制,可减少误差传播,但建模难度更高。
点预测 vs 概率预测 (Point vs. Probabilistic Forecasting): 根据预测结果的性质,时序预测任务可以划分为点预测(非概率)和概率预测,前者为每个时间步生成一个确定性的预测,而后者挖掘数据中的固有不确定性以生成对未来值分布的预测。
二、十大挑战:构建鲁棒预测模型必须面对的现实难题
时间序列数据可以被广泛地定义为按时间顺序收集的序列信号,是一种源自各种传感器或现实世界观察的独特数据模式, 捕捉了系统随时间的动态演变,反映了其短期波动和长期趋势。因此,时序数据展现出数个关键特征,为准确预测提出了挑战。
2.1 数据噪声与异常干扰
时间序列数据常受到传感器误差、人为干预或自然异常事件影响,产生噪声与异常点,严重干扰模型学习。尽管已有大量填补与检测算法,但主流研究多基于理想化干净数据,真实应用场景中仍需提升模型的容错与纠错能力。
2.2 不规则采样与缺失值问题
现实采集场景中由于传输丢包、设备故障或经济成本约束,时间序列往往呈现不规则采样或关键值缺失。如何重构这些数据片段,并充分利用时间间隔信息,成为处理异质时间序列的关键技术问题。
2.3 长期依赖建模困难
长序列预测面临信息稀释、误差积累与依赖衰减等挑战,常规模型难以稳定捕捉远距离信息。需要设计具备更强记忆能力或结构重用机制的模型结构,以突破长期预测的性能瓶颈。
2.4 多变量相关性建模复杂
多变量序列存在潜在的非线性、动态因果关系,变量间的交互往往缺乏明确先验信息。如何在数据驱动条件下学习跨通道依赖关系,是提高预测准确性的核心路径。
2.5 外生变量建模机制不足
预测结果常受外部因素影响,例如节假日、天气、政策等,这些变量具有异步性与非线性作用。目前仍缺乏统一框架来识别关键外因、动态建模其作用,并与目标序列联动优化。
2.6 数据分布漂移阻碍泛化能力
时间序列往往非平稳,不同时间段的统计特性可能发生剧烈变化。分布漂移不仅削弱模型的泛化能力,还可能导致训练数据与预测目标严重不一致,是构建健壮模型必须应对的问题。
2.7 趋势与季节性模式建模复杂
多周期叠加、突变结构、非线性趋势使得传统的趋势/季节性建模方法难以准确表达结构特性。需要更具表达能力的分解方法与数据增强策略辅助模型捕捉多级周期模式。
2.8 多尺度结构融合困难
时间序列存在局部扰动与全局趋势的多层次结构,不同粒度之间的平衡与融合直接影响预测结果。如何在建模过程中有效整合多尺度特征,是提升模型泛化与准确性的关键手段。
2.9 高计算开销限制落地效率
任务维度提升与序列延长导致预测模型计算复杂度剧增,严重影响部署与实时推理效率。在保持预测准确性的同时压缩模型结构,是工业应用中尤为关键的优化目标。
2.10 跨场景泛化与迁移能力薄弱
时间序列缺乏通用语义单元,不同任务之间变量含义、结构特性差异巨大,限制了模型的迁移与重用能力。构建可跨任务泛化的基础模型仍是当前研究的重大挑战之一。
三、数据预处理:构建高质量输入的关键步骤
高质量的输入是构建鲁棒、稳定、可泛化时间序列预测模型的基础。面对真实数据中普遍存在的缺失、噪声、分布变化等问题,科学合理的预处理流程对于提升模型性能、减少训练难度具有重要意义。
3.1 缺失值填补(Imputation)
实际采集中由于传感器故障、通信中断或外部条件影响,时间序列数据中常出现局部或结构性缺失。缺失值不仅导致上下文信息丢失,还会破坏时序结构的连续性,对模型造成严重误导。高质量填补策略不仅能够修复观测序列,还能为下游预测模型提供更完整的历史上下文:
预测式方法:利用已有数据直接预测缺失片段,常用模型包括 RNN、Transformer 等序列建模架构;
生成式方法:引入数据生成机制,使用 GAN、扩散模型等对缺失片段建模,能更好地量化不确定性与多样性。
3.2 去噪处理(Denoising)
即便数据无缺失,也常被设备误差、环境扰动等因素引入高频噪声,这些干扰信号会削弱模型对真实模式的学习能力。优质的去噪策略有助于模型专注于长期趋势和关键变化点,提高预测稳定性与泛化能力:
经典滤波方法:如移动平均、高通/低通滤波,适用于平滑局部震荡;
分解型方法:如小波变换(DWT)、经验模态分解(EMD),将序列拆解为多尺度信号,分别处理噪声;
学习型方法:训练神经网络(如自编码器、Diffusion Model)在有噪-无噪对比中学习降噪映射函数。
3.3 标准化与稳态化(Normalization & Stationarization)
时间序列数据常存在量纲差异、尺度悬殊以及分布动态变化等问题,直接影响模型训练的收敛性与稳定性。通过合理的归一/稳态化策略,不仅提升了模型的数值稳定性,也缓解了不同通道/时间段间的分布漂移问题:
标准化(Normalization):常用 Z-score、Min-Max 或 Log 变换,将各变量统一至可对比的数值范围;
样本归一(Instance Normalization):如 RevIN 对每个样本进行归一与还原,减少非平稳性对模型的影响;
动态归一化方法:如 DAIN、SAN 等,引入可学习参数,根据上下文自适应进行归一处理。
3.4 时间序列分解(Decomposition)
许多时间序列具有明确的趋势(trend)、季节性(seasonality)和噪声(residual)结构。直接预测原始序列容易混淆信号与干扰,因此将其拆解成多个结构性分量有助于建模。分解后的分量可分别建模并独立预测,最终再组合为整体结果,从而提升预测准确率与可解释性:
加性模型(EMD, STL, LMD ):适用于成分可加的序列,结构清晰、适用面广;
乘性模型(VMD, Wavelet Transform, SSA):适合对周期成分强的金融、气象类数据;
3.5 时序片段化表示(Tokenization)
将原始时间序列转换为模型可处理的 token 结构是近年来的研究热点,借鉴 NLP 与视觉领域的成功经验,有效提升模型的表达力与泛化能力。Tokenization 技术有效提升了输入结构的表达能力,是构建“类语言”时间序列模型的重要基础:
连续 tokenization:Point-wise方法以每个时间点作为独立 token,简单直接但信息稀疏;而Patch-wise的方法将连续时间段打包成 patch,如 PatchTST,通过学习局部上下文提升建模质量。
改进型 patchify:如 deformable patchify 可自适应学习 patch 边界,多尺度 patchify 则引入不同尺度融合机制。
离散 tokenization:如使用向量量化(VQ-VAE)将连续值映射为有限字典中的离散符号;或使用统计离散分桶(如按分位数)进行符号化,利于下游多模态融合与大模型建模。
3.6 频率变换(Frequency Transformation)
时间序列的周期性和局部变化在频域中具有更清晰的表现,因此频率分析在建模中具有独特优势。频率域特征不仅能增强模型对周期、节律的捕捉能力,也常作为输入分支与时域建模联合训练,提高模型整体表现:
DFT / DCT:适用于分析平稳数据中的主频成分;
STFT:局部滑窗处理,适合处理局部平稳但整体变化的时序;
DWT:具备良好的时频局部性,能同时捕捉趋势与突变,广泛应用于金融与生理信号分析。
3.7 图结构建模(Graph Transformation)
多变量时间序列中,各通道间的依赖关系可能是复杂的拓扑结构,仅依靠堆叠通道建模容易忽视这种结构性。结合图神经网络(如 GCN、GAT、STGCN)可以进一步学习空间依赖与时序演化双重信息,提升模型对复杂多变量系统的理解能力:
启发式图构建:通过先验知识、空间距离、Pearson 相关或 DTW 相似度构建静态图结构;
学习式图建模:采用神经网络动态学习变量间关系图,支持可微优化与结构自适应;
动态图或时变图:建模变量关系随时间变化的演化过程,更贴近现实系统行为。
四、模型方法全景:从统计建模到生成模型
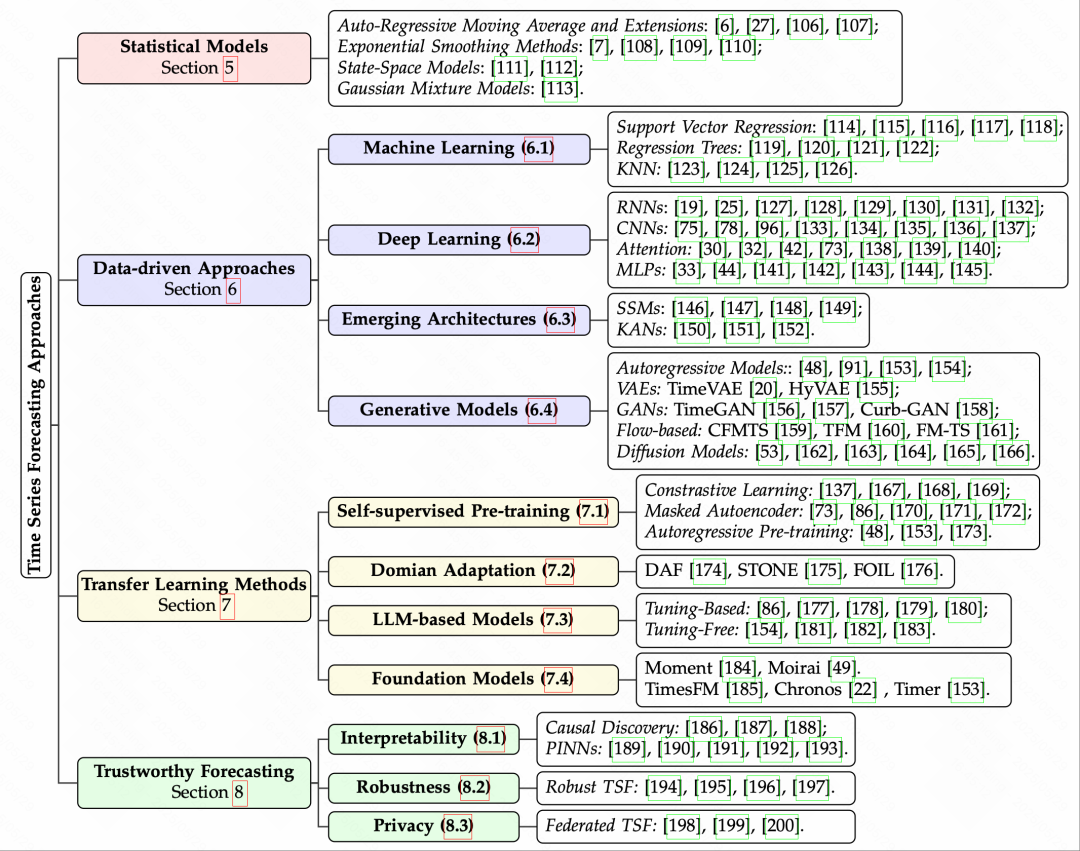
时间序列预测方法模型经历了从统计学模型、机器学习方法,到深度学习与生成建模的演进路径。不同方法各有适应场景与建模能力,构成了多层次的技术图谱。在实际应用中,往往需根据任务特性、数据规模、计算资源进行合理选择与组合。
4.1 统计建模方法
自回归与滑动平均模型:早期时间序列建模主要依赖线性假设,AR模型通过历史值加权预测未来,MA模型则利用过去误差的加权组合。ARMA 结合二者优点,适合处理平稳性时间序列,形式简洁、推导清晰。ARIMA 引入差分操作解决非平稳问题,是广泛使用的通用统计预测模型。SARIMA 扩展出季节性建模能力,支持多个周期嵌套,对交通、销量等季节规律明显的数据表现出色。
指数平滑方法:通过对新旧数据分配权重进行趋势建模,简单指数平滑(SES)适用于无趋势/周期的短期预测,Holt 方法引入趋势建模,Holt-Winters 方法进一步加入季节性因子,适合周期明显的数据。
状态空间模型:状态空间模型以“隐变量 + 观测值”方式建模系统动态演化过程,具备理论严谨性和强泛化能力。Kalman Filter 在线性高斯假设下实现精确滤波,HMM 将状态空间离散化,适合建模跳变系统和隐性状态过程。
高斯混合模型:GMM 将复杂分布建模为多个高斯分布加权组合,适合处理结构变化频繁的时间序列。其可用于建模多模态预测结果、检测结构性异常,常作为密度估计或聚类组件嵌入到预测框架中。
4.2 传统机器学习方法
支持向量回归:SVR 在高维空间中拟合边界内误差最小的函数,适合中等样本规模与较强非线性的数据。通过核函数映射能有效捕捉复杂关系,常用于金融市场、空气质量等预测任务中。
回归树与集成模型:树模型通过递归划分特征空间拟合目标变量,结构清晰、训练高效。集成学习(如 RF、GBDT)通过多棵树组合提升准确率与鲁棒性,XGBoost、LightGBM 等模型在工业竞赛中表现优异,适用于建模非线性与交互关系。
K近邻回归:KNN 基于“最近邻”的思想进行预测,无需显式建模过程。适用于重复模式明显或季节性强的序列,但计算复杂度随数据量增加而上升,适合小规模任务。
4.3 深度学习方法
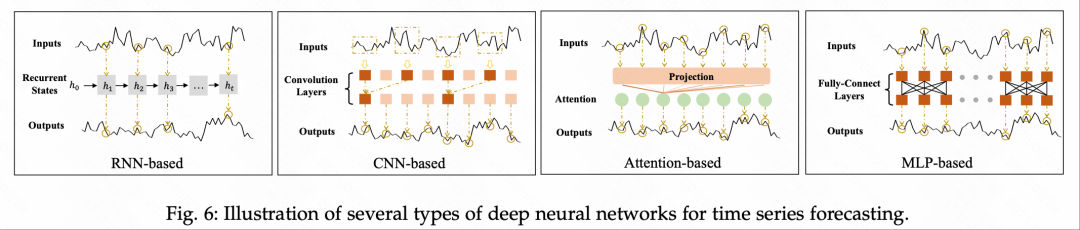
循环神经网络:RNN 以递归方式处理序列,在序列建模早期表现突出,但存在梯度消失、长期依赖捕捉能力差等问题。LSTM 和 GRU 引入门控机制后显著增强了长期信息保留能力,仍是医疗监测、金融建模等领域的重要基线。在此基础上,DeepAR结合 LSTM + 概率分布输出,用于多任务共享建模和生成未来采样;SegRNN则是采用了通道解耦建模策略,用GRU建模时间片上的依赖关系。
卷积神经网络:CNN 利用局部感受野高效提取时序片段中的形态模式,适合处理短期高频变化。TCN(时序卷积网络)使用因果卷积与空洞结构扩大感受野,具备与 RNN 类似的长期依赖建模能力,同时支持更好的并行性。LSTNet融合卷积神经网络与循环神经网络,同时建模局部模式和长期依赖;SCINet基于分治策略拆分序列并重建,有效提升长序列预测精度;而TimesNet融合时间卷积与多尺度块设计,实现通用的表征学习。
Transformer模型:通过自注意力机制建模任意位置之间的关系,具备天然的长期依赖建模能力。为适配时间序列,研究者提出多种结构优化策略:Autoformer / FEDformer引入时间序列分解机制、频率建模机制,压缩注意力计算开销;PatchTST从序列切片的角度式建模上下文;Non-stationary Transformer引入可学习的归一化层,适配非平稳分布。
多层感知机:MLP模型结构简单,易于训练,近年来通过结构创新焕发新活力。N-HiTS / TimeMixer引入多尺度抽样、时间滤波器提升建模能力;SparseTSF / FITS则是探索了极限参数压缩(<1k)下的模型预测能力。
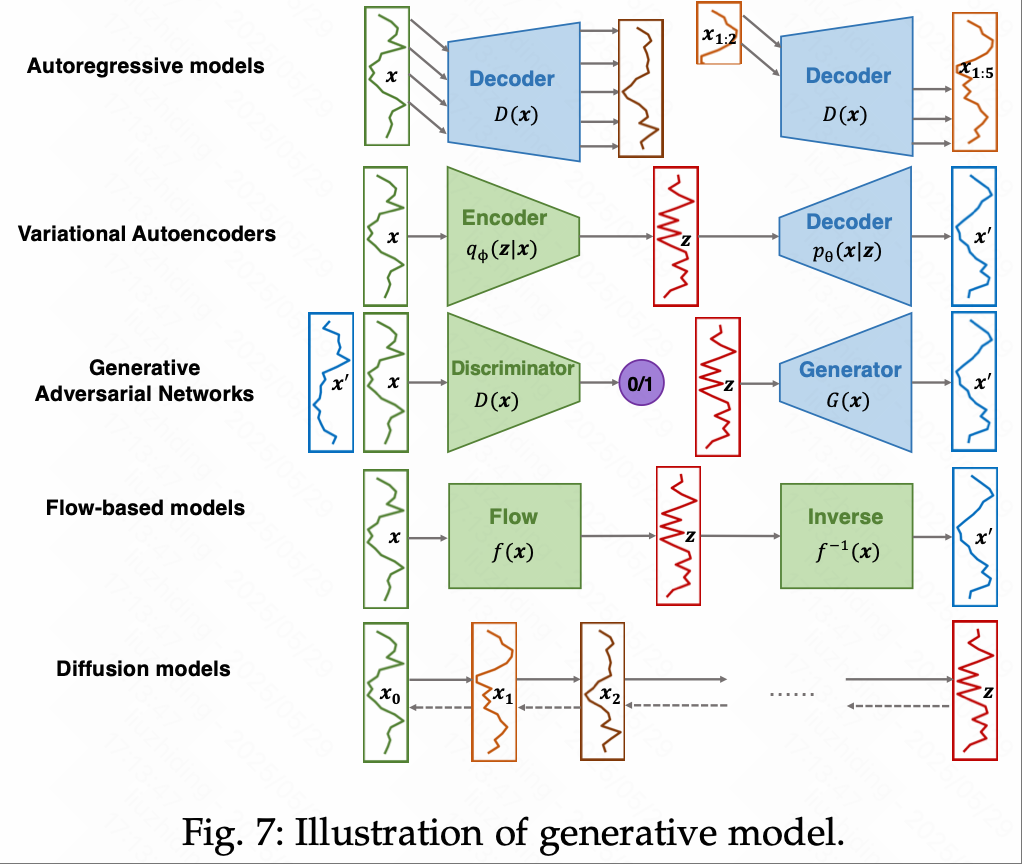
4.4 生成模型
变分自编码器:VAE 通过学习潜在空间中的分布实现重构与生成,可用于概率预测与不确定性建模。TimeVAE 引入时间条件向量,HyVAE 支持多个模态协同生成,广泛用于医疗与金融风险分析。
生成对抗网络:GAN 利用生成器与判别器博弈学习数据分布,适用于生成高质量拟真序列。TimeGAN 结合监督信号保留时间顺序特征,Curb-GAN 在电力与交通场景中展现出良好的数据增强效果。
流模型:流模型通过可逆变换对数据建模,具有明确的密度函数表示,适合概率预测与异常检测。FM-TS 结合频率域结构建模复杂分布,CFMTS 使用耦合变换处理高维序列数据。
扩散模型:扩散模型基于逐步加噪/去噪的过程建模数据生成路径,使得模型能够学习复杂的数据分布并生成高质量的预测,适用于多模态、多样性要求高的场景。TSDiff 通过自我引导提高了短期准确性和数据生成效率;LDT利用潜在扩散模型在降水预报和可扩展性方面都展示了显著的改进。
五、学习范式演进:可迁移、可信的时序预测方法
5.1 自监督学习
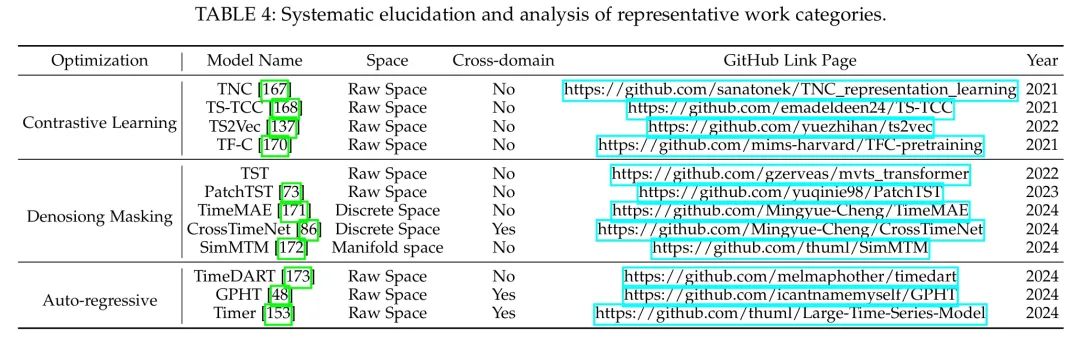
对比学习:对比学习通过构造正负样本对,促使模型学习具有判别性的时序表示。在时间序列任务中,对比学习通常结合数据增强策略(如扰动、时间裁剪、遮蔽)以构造多样化的样本视角,从而提升模型在不同场景下的泛化能力。TS2Vec 是时间序列中较早的通用对比学习框架,为无监督特征表示学习奠定了基础。在此基础上,TNC 与 TS-TCC 进一步提升了模型对时间序列中关键特征的提取能力。
掩码自编码器: 掩码自编码器通过有策略地遮蔽部分输入数据,并重建被遮蔽区域,引导模型学习鲁棒的特征表示。在原始数据空间中,TST首次将掩码自编码机制引入时间序列;在离散潜在空间中,TimeMAE与 CrossTimeNet将时间序列映射到统一的离散表示形式,便于跨领域的自监督预训练;SimMTM通过加权聚合相邻时间片的方式重建被遮蔽的时间点,在流行空间中实现了更加结构化的语义建模。
自回归式预训练:自回归模型通过利用历史数据预测未来值,从而捕捉时间序列中的动态变化和时序依赖关系。在时间序列预训练中,自回归机制能够逐步建模序列的演化过程。TimeDART 将时间序列划分为多个数据块,并以 Transformer 编码器建模块间依赖,同时结合扩散与去噪机制,提取块内的细粒度特征,实现了扩散模型在时间序列中的有效应用;Timer 则统一不同类型的时间序列为一种通用格式(S3),并采用 GPT 风格的解码器架构,展现出良好的扩展性与泛化能力。
5.2 领域自适应
由于分布变化(distribution shift)广泛存在于时间序列数据中,导致模型在新领域上预测效果下降,形成典型的“分布外”(OOD)问题。同时,不同领域间序列特征的映射关系往往差异显著,给模型迁移带来额外挑战。因此,提升时间序列预测的可迁移性,核心在于实现有效的领域自适应机制。SLARDA 通过自监督对比预训练,学习更具迁移性的时序表示,同时兼顾时间动态性与特征对齐;FOIL设计替代损失函数与联合优化策略,在存在未观测变量时仍能学习稳定表示,进一步提升 OOD 时间序列的泛化能力。
5.3 基于语言模型的预测方法
近年来,大语言模型(LLMs)因其强大的语义理解与推理能力,被广泛探索用于时间序列预测任务。这类方法可以将时间序列数据转换为类似文本的输入格式,并借助预训练语言模型进行预测。相比传统模型,LLM 更擅长结合结构化信息与文本上下文,如个体特征或采样背景,从而提升预测准确性。
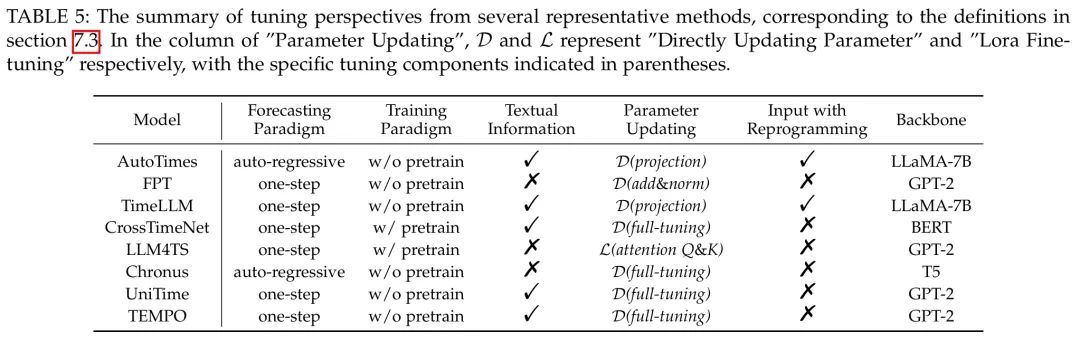
参数调优型方法:通过对预训练模型进行微调,使其更贴合特定时间序列数据。为实现高质量预测,研究者从多个角度提出创新策略。
-
预测方式上,如 AutoTimes 使用自回归(Auto-regressive)方式逐步生成序列,而 FPT 则采用一跳预测(One-step)方式一次性生成完整序列,以减少误差累积。
-
训练范式上,CrossTimeNet 引入自监督预训练,提升模型对时间序列结构的理解。
-
文本融合上,如 TEMPO 结合结构化数据与文本输入,让模型利用自然语言信息辅助预测。
-
参数更新方式上,LLM4TS 采用 LoRA 策略对核心模块低秩微调,也有部分模型直接更新主干参数。
-
输入表示上,Chronos 和 UniTime 采用嵌入后的结构化输入,TimeLLM 则融合时序与文本特征,提升输入信息丰富度。
零调优型方法:该类方法无需修改语言模型参数,直接通过 Prompt 构造完成预测任务,具有部署灵活、成本低等优势。
-
Prompt设计方面,如 LLMTime 将样本背景转为文本信息输入模型,LSTPrompt 引入「思考间歇」机制模拟人类预测过程。
-
上下文增强方面,TimeRAF 采用检索增强生成(RAG)策略,基于相似历史样本构造 Prompt;TimeRAG 将检索样本转化为 JSON 输入,提升推理效果。
-
跨模态理解上,TableTime 验证了 LLaMA 等模型对表格时序数据的理解与分类能力。
-
智能体协作上,TESSA 利用通用与专业注释智能体,提升 GPT-4o 对时间序列的语义解析与推理能力
-
挑战方面,Merrill 等人发现当前零调优模型的预测能力有限,部分任务甚至接近随机水平,表明“时间序列推理”在 LLM 中仍处于早期发展阶段。
5.4 时间序列基座模型构建
近年来,时间序列基础模型在大规模时序数据上预训练后崭露头角,凭借其强大的跨领域泛化能力,正在重塑时间序列预测任务的技术格局。Moirai引入面向任意变量的注意力机制,在大规模 LOTSA 数据集上通过掩码预训练,展现出优异的跨分布预测能力;Timer进一步统一多种预测任务,采用 GPT 式自回归结构,展示出强大的通用预测能力。
尽管结构各异,这些模型都秉持“简洁通用”的设计理念,避免对特定任务的过拟合。当前的发展重点主要集中在:
这些趋势标志着时间序列研究正逐步迈向数据驱动(data-centric)的新范式,在基础模型与下游任务之间建立更稳固的桥梁。
-
构建大规模、跨领域的预训练数据集(如 LOTSA 数据集包含 270 亿时间步);
-
探索统一建模框架以适配多变量分析;
-
利用合成数据提升泛化能力,例如 TimesFM 的训练数据中有 20% 来自合成样本。
5.5 可解释性
可信预测模型不仅要有准确的结果,还应回答“为什么会这么预测”。当前提升预测模型可解释性的主流研究聚焦在两个方向:因果发现(Causal Discovery)和物理引导神经网络(PINNs)。
因果发现方法试图揭示变量之间潜在的因果关系,帮助模型更清晰地识别时间序列中的驱动因素。例如,Granger 因果性分析、动态贝叶斯网络等传统方法为因果推断提供了统计基础,近年来更有融合深度学习的因果建模方式,用于处理非线性与非平稳序列。在复杂系统中,这类方法显著提升了模型的解释能力与泛化性能。
另一方面,PINNs通过将微分方程、守恒定律等物理知识直接嵌入模型结构中,使得预测不仅符合历史数据,也满足自然规律。这种融合物理约束的方式在科学计算、工程建模等领域尤其重要,能够有效应对数据稀疏或噪声干扰,提升模型的可信度和适用性。
5.6 鲁棒性
当前时间序列模型在预测精度上取得了长足进展,但它们对输入扰动仍较敏感,容易受到对抗攻击的干扰,进而产生严重后果。
部分研究提出通过蒙特卡洛估计目标序列分布,生成具有隐蔽性和欺骗性的攻击样本,专门攻击概率型预测模型。针对更具现实性的稀疏攻击场景,学者们发展出如随机平滑与对抗训练等防御机制,在保留模型性能的同时提高鲁棒性。更进一步,像 RDAT 引入强化学习与自蒸馏策略,有效增强了交通预测任务中的防御效果。
此外,BACKTIME 揭示了主流预测模型在面临后门攻击时的脆弱性。这类攻击通过在训练数据中植入稀疏触发器,在预测阶段以极小代价触发错误输出,提示我们必须加强对时序模型安全性的关注与治理。
5.7 隐私保护
大规模预训练已成为时间序列建模的新趋势,但如何在整合多源数据的同时保护用户隐私,成为不可回避的挑战。为此,研究者积极引入联邦学习框架,推动隐私友好的时序预测研究。
例如,CNFGNN 将图结构编码与跨节点联邦学习相结合,在不直接共享数据的前提下建模复杂的空间-时间依赖关系。MetePFL 则引入提示学习机制,并结合图模型减轻多源数据之间的异质性带来的影响。Time-FFM 更进一步构建了融合语言模型与联邦架构的时序基础模型,通过分离全局编码与本地预测模块,在确保隐私的同时保持高度个性化的预测能力。
随着数据合规监管的加强,联邦学习等隐私保护机制将成为可信时序模型发展的重要基石,为实际落地提供可行路径。
六、未来趋势:推动预测从“准”走向“智”
随着时间序列预测在基础模型、可信建模、训练范式等方面不断取得突破,未来的研究将更加多元、深入并面向实际落地,推动预测从“准”走向“智”。
6.1 时间序列基础模型:迈向通用智能的基石
借鉴计算机视觉与自然语言处理领域基础模型的成功经验,构建适用于时间序列分析的“通用基础模型”已成为新的研究热点。虽然已有诸如TimesFM、Chronos等探索取得初步进展,但当前模型仍存在上下文理解不充分、泛化能力有限等问题。
在数据层面,不同领域的时序数据存在采样频率差异、噪声水平不同,甚至物理含义各异,建立统一的语义表示亟需深入研究。同时,即使同属一个领域,不同对象(如不同患者或城市)间的时序数据也可能展现出明显的个体差异。此外,不同任务对预测结果的需求各异,模型应具备按需响应和指令适应能力。未来研究亟需探索如何引入文本、图像、图结构等多模态数据,帮助模型更全面地理解和建模复杂的上下文信息。
与此同时,是否存在一个“真正通用”的时间序列基础模型仍是开放问题,也激发了多种探索方向:如基础模型的扩展规律(scaling laws)与能力涌现(emergence)机制研究,不同比例数据对模型能力的影响评估,乃至开发面向特定领域(如医疗、交通等)的定制型基础模型,融合领域知识实现更精准的预测。
6.2 可信时间序列预测:让AI值得信赖
现有大多数预测模型为深度神经网络,虽然具备强大表达能力,但往往难以解释预测原因,不适用于对安全性与可解释性有高要求的场景(如医疗辅助诊断)。未来应当探索将可解释AI(XAI)与因果推理等技术与强预测模型融合,构建“既能预测准,又能说明白”的可信模型。
另一方面,训练跨域模型往往需要汇聚来自多源的数据,如何在提升性能的同时保障用户隐私与系统安全成为关键挑战。当前主流方法多借助联邦学习框架,但如何引入差分隐私等机制来防止数据泄露、如何增强模型抵抗“恶意客户端投毒”等攻击,仍是亟需解决的重要课题,关乎大规模部署可信AI的可行性。
6.3 新型建模范式:从“结构设计”走向“范式革命”
时间序列预测向来是一个开放且包容的研究领域,不同网络结构、训练策略与视角的不断尝试,推动了整体技术生态的演进。近年来,许多前沿机器学习技术也正逐步渗透进时序预测中,带来了新的范式变革机遇。
例如,可探索如何引入AutoML方法,自动调整网络结构、权衡预测精度与计算效率,提升模型在实际部署中的适用性。又如,物理引导神经网络(PINNs)作为一种嵌入先验知识的方式,能够有效应对数据稀缺问题,增强模型的可靠性和可解释性。将这些“跨界”方法与时序预测相融合,预计将为该领域注入新的活力与思维方式。
6.4 全面评估体系:推动模型发展从“跑分”到“认知”
除了模型架构本身,如何科学、公平地评估时序模型的性能也是推动整个领域健康发展的关键。当前主流评估基准普遍面临分布单一、任务难度区分不清的问题,评价指标也多为单一误差指标,难以全面反映模型优势与局限。
这不仅可能引发“跑分竞赛”,更可能掩盖模型在泛化能力、稳定性、计算效率等方面的真实表现。因此,未来需要构建覆盖多分布、多任务、多场景的通用评估数据集,同时引入多元评价维度(如鲁棒性、泛化性、效率等),以促使模型设计更加全面、务实、稳健。
一、基础概念与定义:时间序列预测的底层逻辑
回顾窗口(Look-back Window):指目标时间序列中最近 L 个时间步的连续观测值,作为主要的历史上下文信息来源,用于建模趋势、季节性和其他时间依赖关系。
协变量(Covariates / 外生变量):除目标序列外,许多应用还利用气象、经济或人口等外部因素作为辅助输入。这些变量有助于提升模型对外部驱动因素的建模能力。
预测窗口(Predicted Window):预测任务的输出通常是一段未来时间步,长度可以从单步(如下一小时)到多步(如下一周或下月)不等。
单步 vs 多步预测(One-step vs. Multi-step):单步预测每次仅预测一个未来时间点,适用于逐步滚动预测;多步预测则一次性输出多个未来时间点,能够建模长期依赖,但可能引入更大的误差累积。
单变量 vs 多变量预测(Univariate vs. Multivariate):单变量预测仅依赖目标序列本身;多变量预测则引入多个相关序列或协变量,以挖掘跨序列间的依赖关系,从而提升精度。
迭代 vs 直接预测策略(Iterative vs. Direct Strategies):迭代策略逐步生成未来值,并将其作为输入用于后续预测;直接策略则为每个未来时间步构建独立的预测机制,可减少误差传播,但建模难度更高。
点预测 vs 概率预测 (Point vs. Probabilistic Forecasting): 根据预测结果的性质,时序预测任务可以划分为点预测(非概率)和概率预测,前者为每个时间步生成一个确定性的预测,而后者挖掘数据中的固有不确定性以生成对未来值分布的预测。
二、十大挑战:构建鲁棒预测模型必须面对的现实难题
时间序列数据可以被广泛地定义为按时间顺序收集的序列信号,是一种源自各种传感器或现实世界观察的独特数据模式, 捕捉了系统随时间的动态演变,反映了其短期波动和长期趋势。因此,时序数据展现出数个关键特征,为准确预测提出了挑战。
2.1 数据噪声与异常干扰
时间序列数据常受到传感器误差、人为干预或自然异常事件影响,产生噪声与异常点,严重干扰模型学习。尽管已有大量填补与检测算法,但主流研究多基于理想化干净数据,真实应用场景中仍需提升模型的容错与纠错能力。
2.2 不规则采样与缺失值问题
现实采集场景中由于传输丢包、设备故障或经济成本约束,时间序列往往呈现不规则采样或关键值缺失。如何重构这些数据片段,并充分利用时间间隔信息,成为处理异质时间序列的关键技术问题。
2.3 长期依赖建模困难
长序列预测面临信息稀释、误差积累与依赖衰减等挑战,常规模型难以稳定捕捉远距离信息。需要设计具备更强记忆能力或结构重用机制的模型结构,以突破长期预测的性能瓶颈。
2.4 多变量相关性建模复杂
多变量序列存在潜在的非线性、动态因果关系,变量间的交互往往缺乏明确先验信息。如何在数据驱动条件下学习跨通道依赖关系,是提高预测准确性的核心路径。
2.5 外生变量建模机制不足
预测结果常受外部因素影响,例如节假日、天气、政策等,这些变量具有异步性与非线性作用。目前仍缺乏统一框架来识别关键外因、动态建模其作用,并与目标序列联动优化。
2.6 数据分布漂移阻碍泛化能力
时间序列往往非平稳,不同时间段的统计特性可能发生剧烈变化。分布漂移不仅削弱模型的泛化能力,还可能导致训练数据与预测目标严重不一致,是构建健壮模型必须应对的问题。
2.7 趋势与季节性模式建模复杂
多周期叠加、突变结构、非线性趋势使得传统的趋势/季节性建模方法难以准确表达结构特性。需要更具表达能力的分解方法与数据增强策略辅助模型捕捉多级周期模式。
2.8 多尺度结构融合困难
时间序列存在局部扰动与全局趋势的多层次结构,不同粒度之间的平衡与融合直接影响预测结果。如何在建模过程中有效整合多尺度特征,是提升模型泛化与准确性的关键手段。
2.9 高计算开销限制落地效率
任务维度提升与序列延长导致预测模型计算复杂度剧增,严重影响部署与实时推理效率。在保持预测准确性的同时压缩模型结构,是工业应用中尤为关键的优化目标。
2.10 跨场景泛化与迁移能力薄弱
时间序列缺乏通用语义单元,不同任务之间变量含义、结构特性差异巨大,限制了模型的迁移与重用能力。构建可跨任务泛化的基础模型仍是当前研究的重大挑战之一。
三、数据预处理:构建高质量输入的关键步骤
高质量的输入是构建鲁棒、稳定、可泛化时间序列预测模型的基础。面对真实数据中普遍存在的缺失、噪声、分布变化等问题,科学合理的预处理流程对于提升模型性能、减少训练难度具有重要意义。
3.1 缺失值填补(Imputation)
实际采集中由于传感器故障、通信中断或外部条件影响,时间序列数据中常出现局部或结构性缺失。缺失值不仅导致上下文信息丢失,还会破坏时序结构的连续性,对模型造成严重误导。高质量填补策略不仅能够修复观测序列,还能为下游预测模型提供更完整的历史上下文:
预测式方法:利用已有数据直接预测缺失片段,常用模型包括 RNN、Transformer 等序列建模架构;
生成式方法:引入数据生成机制,使用 GAN、扩散模型等对缺失片段建模,能更好地量化不确定性与多样性。
3.2 去噪处理(Denoising)
即便数据无缺失,也常被设备误差、环境扰动等因素引入高频噪声,这些干扰信号会削弱模型对真实模式的学习能力。优质的去噪策略有助于模型专注于长期趋势和关键变化点,提高预测稳定性与泛化能力:
经典滤波方法:如移动平均、高通/低通滤波,适用于平滑局部震荡;
分解型方法:如小波变换(DWT)、经验模态分解(EMD),将序列拆解为多尺度信号,分别处理噪声;
学习型方法:训练神经网络(如自编码器、Diffusion Model)在有噪-无噪对比中学习降噪映射函数。
3.3 标准化与稳态化(Normalization & Stationarization)
时间序列数据常存在量纲差异、尺度悬殊以及分布动态变化等问题,直接影响模型训练的收敛性与稳定性。通过合理的归一/稳态化策略,不仅提升了模型的数值稳定性,也缓解了不同通道/时间段间的分布漂移问题:
标准化(Normalization):常用 Z-score、Min-Max 或 Log 变换,将各变量统一至可对比的数值范围;
样本归一(Instance Normalization):如 RevIN 对每个样本进行归一与还原,减少非平稳性对模型的影响;
动态归一化方法:如 DAIN、SAN 等,引入可学习参数,根据上下文自适应进行归一处理。
3.4 时间序列分解(Decomposition)
许多时间序列具有明确的趋势(trend)、季节性(seasonality)和噪声(residual)结构。直接预测原始序列容易混淆信号与干扰,因此将其拆解成多个结构性分量有助于建模。分解后的分量可分别建模并独立预测,最终再组合为整体结果,从而提升预测准确率与可解释性:
加性模型(EMD, STL, LMD ):适用于成分可加的序列,结构清晰、适用面广;
乘性模型(VMD, Wavelet Transform, SSA):适合对周期成分强的金融、气象类数据;
3.5 时序片段化表示(Tokenization)
将原始时间序列转换为模型可处理的 token 结构是近年来的研究热点,借鉴 NLP 与视觉领域的成功经验,有效提升模型的表达力与泛化能力。Tokenization 技术有效提升了输入结构的表达能力,是构建“类语言”时间序列模型的重要基础:
连续 tokenization:Point-wise方法以每个时间点作为独立 token,简单直接但信息稀疏;而Patch-wise的方法将连续时间段打包成 patch,如 PatchTST,通过学习局部上下文提升建模质量。
改进型 patchify:如 deformable patchify 可自适应学习 patch 边界,多尺度 patchify 则引入不同尺度融合机制。
离散 tokenization:如使用向量量化(VQ-VAE)将连续值映射为有限字典中的离散符号;或使用统计离散分桶(如按分位数)进行符号化,利于下游多模态融合与大模型建模。
3.6 频率变换(Frequency Transformation)
时间序列的周期性和局部变化在频域中具有更清晰的表现,因此频率分析在建模中具有独特优势。频率域特征不仅能增强模型对周期、节律的捕捉能力,也常作为输入分支与时域建模联合训练,提高模型整体表现:
DFT / DCT:适用于分析平稳数据中的主频成分;
STFT:局部滑窗处理,适合处理局部平稳但整体变化的时序;
DWT:具备良好的时频局部性,能同时捕捉趋势与突变,广泛应用于金融与生理信号分析。
3.7 图结构建模(Graph Transformation)
多变量时间序列中,各通道间的依赖关系可能是复杂的拓扑结构,仅依靠堆叠通道建模容易忽视这种结构性。结合图神经网络(如 GCN、GAT、STGCN)可以进一步学习空间依赖与时序演化双重信息,提升模型对复杂多变量系统的理解能力:
启发式图构建:通过先验知识、空间距离、Pearson 相关或 DTW 相似度构建静态图结构;
学习式图建模:采用神经网络动态学习变量间关系图,支持可微优化与结构自适应;
动态图或时变图:建模变量关系随时间变化的演化过程,更贴近现实系统行为。
四、模型方法全景:从统计建模到生成模型
时间序列预测方法模型经历了从统计学模型、机器学习方法,到深度学习与生成建模的演进路径。不同方法各有适应场景与建模能力,构成了多层次的技术图谱。在实际应用中,往往需根据任务特性、数据规模、计算资源进行合理选择与组合。
4.1 统计建模方法
自回归与滑动平均模型:早期时间序列建模主要依赖线性假设,AR模型通过历史值加权预测未来,MA模型则利用过去误差的加权组合。ARMA 结合二者优点,适合处理平稳性时间序列,形式简洁、推导清晰。ARIMA 引入差分操作解决非平稳问题,是广泛使用的通用统计预测模型。SARIMA 扩展出季节性建模能力,支持多个周期嵌套,对交通、销量等季节规律明显的数据表现出色。
指数平滑方法:通过对新旧数据分配权重进行趋势建模,简单指数平滑(SES)适用于无趋势/周期的短期预测,Holt 方法引入趋势建模,Holt-Winters 方法进一步加入季节性因子,适合周期明显的数据。
状态空间模型:状态空间模型以“隐变量 + 观测值”方式建模系统动态演化过程,具备理论严谨性和强泛化能力。Kalman Filter 在线性高斯假设下实现精确滤波,HMM 将状态空间离散化,适合建模跳变系统和隐性状态过程。
高斯混合模型:GMM 将复杂分布建模为多个高斯分布加权组合,适合处理结构变化频繁的时间序列。其可用于建模多模态预测结果、检测结构性异常,常作为密度估计或聚类组件嵌入到预测框架中。
4.2 传统机器学习方法
支持向量回归:SVR 在高维空间中拟合边界内误差最小的函数,适合中等样本规模与较强非线性的数据。通过核函数映射能有效捕捉复杂关系,常用于金融市场、空气质量等预测任务中。
回归树与集成模型:树模型通过递归划分特征空间拟合目标变量,结构清晰、训练高效。集成学习(如 RF、GBDT)通过多棵树组合提升准确率与鲁棒性,XGBoost、LightGBM 等模型在工业竞赛中表现优异,适用于建模非线性与交互关系。
K近邻回归:KNN 基于“最近邻”的思想进行预测,无需显式建模过程。适用于重复模式明显或季节性强的序列,但计算复杂度随数据量增加而上升,适合小规模任务。
4.3 深度学习方法
循环神经网络:RNN 以递归方式处理序列,在序列建模早期表现突出,但存在梯度消失、长期依赖捕捉能力差等问题。LSTM 和 GRU 引入门控机制后显著增强了长期信息保留能力,仍是医疗监测、金融建模等领域的重要基线。在此基础上,DeepAR结合 LSTM + 概率分布输出,用于多任务共享建模和生成未来采样;SegRNN则是采用了通道解耦建模策略,用GRU建模时间片上的依赖关系。
卷积神经网络:CNN 利用局部感受野高效提取时序片段中的形态模式,适合处理短期高频变化。TCN(时序卷积网络)使用因果卷积与空洞结构扩大感受野,具备与 RNN 类似的长期依赖建模能力,同时支持更好的并行性。LSTNet融合卷积神经网络与循环神经网络,同时建模局部模式和长期依赖;SCINet基于分治策略拆分序列并重建,有效提升长序列预测精度;而TimesNet融合时间卷积与多尺度块设计,实现通用的表征学习。
Transformer模型:通过自注意力机制建模任意位置之间的关系,具备天然的长期依赖建模能力。为适配时间序列,研究者提出多种结构优化策略:Autoformer / FEDformer引入时间序列分解机制、频率建模机制,压缩注意力计算开销;PatchTST从序列切片的角度式建模上下文;Non-stationary Transformer引入可学习的归一化层,适配非平稳分布。
多层感知机:MLP模型结构简单,易于训练,近年来通过结构创新焕发新活力。N-HiTS / TimeMixer引入多尺度抽样、时间滤波器提升建模能力;SparseTSF / FITS则是探索了极限参数压缩(<1k)下的模型预测能力。
4.4 生成模型
变分自编码器:VAE 通过学习潜在空间中的分布实现重构与生成,可用于概率预测与不确定性建模。TimeVAE 引入时间条件向量,HyVAE 支持多个模态协同生成,广泛用于医疗与金融风险分析。
生成对抗网络:GAN 利用生成器与判别器博弈学习数据分布,适用于生成高质量拟真序列。TimeGAN 结合监督信号保留时间顺序特征,Curb-GAN 在电力与交通场景中展现出良好的数据增强效果。
流模型:流模型通过可逆变换对数据建模,具有明确的密度函数表示,适合概率预测与异常检测。FM-TS 结合频率域结构建模复杂分布,CFMTS 使用耦合变换处理高维序列数据。
扩散模型:扩散模型基于逐步加噪/去噪的过程建模数据生成路径,使得模型能够学习复杂的数据分布并生成高质量的预测,适用于多模态、多样性要求高的场景。TSDiff 通过自我引导提高了短期准确性和数据生成效率;LDT利用潜在扩散模型在降水预报和可扩展性方面都展示了显著的改进。
五、学习范式演进:可迁移、可信的时序预测方法
5.1 自监督学习
对比学习:对比学习通过构造正负样本对,促使模型学习具有判别性的时序表示。在时间序列任务中,对比学习通常结合数据增强策略(如扰动、时间裁剪、遮蔽)以构造多样化的样本视角,从而提升模型在不同场景下的泛化能力。TS2Vec 是时间序列中较早的通用对比学习框架,为无监督特征表示学习奠定了基础。在此基础上,TNC 与 TS-TCC 进一步提升了模型对时间序列中关键特征的提取能力。
掩码自编码器: 掩码自编码器通过有策略地遮蔽部分输入数据,并重建被遮蔽区域,引导模型学习鲁棒的特征表示。在原始数据空间中,TST首次将掩码自编码机制引入时间序列;在离散潜在空间中,TimeMAE与 CrossTimeNet将时间序列映射到统一的离散表示形式,便于跨领域的自监督预训练;SimMTM通过加权聚合相邻时间片的方式重建被遮蔽的时间点,在流行空间中实现了更加结构化的语义建模。
自回归式预训练:自回归模型通过利用历史数据预测未来值,从而捕捉时间序列中的动态变化和时序依赖关系。在时间序列预训练中,自回归机制能够逐步建模序列的演化过程。TimeDART 将时间序列划分为多个数据块,并以 Transformer 编码器建模块间依赖,同时结合扩散与去噪机制,提取块内的细粒度特征,实现了扩散模型在时间序列中的有效应用;Timer 则统一不同类型的时间序列为一种通用格式(S3),并采用 GPT 风格的解码器架构,展现出良好的扩展性与泛化能力。
5.2 领域自适应
由于分布变化(distribution shift)广泛存在于时间序列数据中,导致模型在新领域上预测效果下降,形成典型的“分布外”(OOD)问题。同时,不同领域间序列特征的映射关系往往差异显著,给模型迁移带来额外挑战。因此,提升时间序列预测的可迁移性,核心在于实现有效的领域自适应机制。SLARDA 通过自监督对比预训练,学习更具迁移性的时序表示,同时兼顾时间动态性与特征对齐;FOIL设计替代损失函数与联合优化策略,在存在未观测变量时仍能学习稳定表示,进一步提升 OOD 时间序列的泛化能力。
5.3 基于语言模型的预测方法
近年来,大语言模型(LLMs)因其强大的语义理解与推理能力,被广泛探索用于时间序列预测任务。这类方法可以将时间序列数据转换为类似文本的输入格式,并借助预训练语言模型进行预测。相比传统模型,LLM 更擅长结合结构化信息与文本上下文,如个体特征或采样背景,从而提升预测准确性。
参数调优型方法:通过对预训练模型进行微调,使其更贴合特定时间序列数据。为实现高质量预测,研究者从多个角度提出创新策略。
-
预测方式上,如 AutoTimes 使用自回归(Auto-regressive)方式逐步生成序列,而 FPT 则采用一跳预测(One-step)方式一次性生成完整序列,以减少误差累积。
-
训练范式上,CrossTimeNet 引入自监督预训练,提升模型对时间序列结构的理解。
-
文本融合上,如 TEMPO 结合结构化数据与文本输入,让模型利用自然语言信息辅助预测。
-
参数更新方式上,LLM4TS 采用 LoRA 策略对核心模块低秩微调,也有部分模型直接更新主干参数。
-
输入表示上,Chronos 和 UniTime 采用嵌入后的结构化输入,TimeLLM 则融合时序与文本特征,提升输入信息丰富度。
零调优型方法:该类方法无需修改语言模型参数,直接通过 Prompt 构造完成预测任务,具有部署灵活、成本低等优势。
-
Prompt设计方面,如 LLMTime 将样本背景转为文本信息输入模型,LSTPrompt 引入「思考间歇」机制模拟人类预测过程。
-
上下文增强方面,TimeRAF 采用检索增强生成(RAG)策略,基于相似历史样本构造 Prompt;TimeRAG 将检索样本转化为 JSON 输入,提升推理效果。
-
跨模态理解上,TableTime 验证了 LLaMA 等模型对表格时序数据的理解与分类能力。
-
智能体协作上,TESSA 利用通用与专业注释智能体,提升 GPT-4o 对时间序列的语义解析与推理能力
-
挑战方面,Merrill 等人发现当前零调优模型的预测能力有限,部分任务甚至接近随机水平,表明“时间序列推理”在 LLM 中仍处于早期发展阶段。
5.4 时间序列基座模型构建
近年来,时间序列基础模型在大规模时序数据上预训练后崭露头角,凭借其强大的跨领域泛化能力,正在重塑时间序列预测任务的技术格局。Moirai引入面向任意变量的注意力机制,在大规模 LOTSA 数据集上通过掩码预训练,展现出优异的跨分布预测能力;Timer进一步统一多种预测任务,采用 GPT 式自回归结构,展示出强大的通用预测能力。
尽管结构各异,这些模型都秉持“简洁通用”的设计理念,避免对特定任务的过拟合。当前的发展重点主要集中在:
这些趋势标志着时间序列研究正逐步迈向数据驱动(data-centric)的新范式,在基础模型与下游任务之间建立更稳固的桥梁。
-
构建大规模、跨领域的预训练数据集(如 LOTSA 数据集包含 270 亿时间步);
-
探索统一建模框架以适配多变量分析;
-
利用合成数据提升泛化能力,例如 TimesFM 的训练数据中有 20% 来自合成样本。
5.5 可解释性
可信预测模型不仅要有准确的结果,还应回答“为什么会这么预测”。当前提升预测模型可解释性的主流研究聚焦在两个方向:因果发现(Causal Discovery)和物理引导神经网络(PINNs)。
因果发现方法试图揭示变量之间潜在的因果关系,帮助模型更清晰地识别时间序列中的驱动因素。例如,Granger 因果性分析、动态贝叶斯网络等传统方法为因果推断提供了统计基础,近年来更有融合深度学习的因果建模方式,用于处理非线性与非平稳序列。在复杂系统中,这类方法显著提升了模型的解释能力与泛化性能。
另一方面,PINNs通过将微分方程、守恒定律等物理知识直接嵌入模型结构中,使得预测不仅符合历史数据,也满足自然规律。这种融合物理约束的方式在科学计算、工程建模等领域尤其重要,能够有效应对数据稀疏或噪声干扰,提升模型的可信度和适用性。
5.6 鲁棒性
当前时间序列模型在预测精度上取得了长足进展,但它们对输入扰动仍较敏感,容易受到对抗攻击的干扰,进而产生严重后果。
部分研究提出通过蒙特卡洛估计目标序列分布,生成具有隐蔽性和欺骗性的攻击样本,专门攻击概率型预测模型。针对更具现实性的稀疏攻击场景,学者们发展出如随机平滑与对抗训练等防御机制,在保留模型性能的同时提高鲁棒性。更进一步,像 RDAT 引入强化学习与自蒸馏策略,有效增强了交通预测任务中的防御效果。
此外,BACKTIME 揭示了主流预测模型在面临后门攻击时的脆弱性。这类攻击通过在训练数据中植入稀疏触发器,在预测阶段以极小代价触发错误输出,提示我们必须加强对时序模型安全性的关注与治理。
5.7 隐私保护
大规模预训练已成为时间序列建模的新趋势,但如何在整合多源数据的同时保护用户隐私,成为不可回避的挑战。为此,研究者积极引入联邦学习框架,推动隐私友好的时序预测研究。
例如,CNFGNN 将图结构编码与跨节点联邦学习相结合,在不直接共享数据的前提下建模复杂的空间-时间依赖关系。MetePFL 则引入提示学习机制,并结合图模型减轻多源数据之间的异质性带来的影响。Time-FFM 更进一步构建了融合语言模型与联邦架构的时序基础模型,通过分离全局编码与本地预测模块,在确保隐私的同时保持高度个性化的预测能力。
随着数据合规监管的加强,联邦学习等隐私保护机制将成为可信时序模型发展的重要基石,为实际落地提供可行路径。
六、未来趋势:推动预测从“准”走向“智”
随着时间序列预测在基础模型、可信建模、训练范式等方面不断取得突破,未来的研究将更加多元、深入并面向实际落地,推动预测从“准”走向“智”。
6.1 时间序列基础模型:迈向通用智能的基石
借鉴计算机视觉与自然语言处理领域基础模型的成功经验,构建适用于时间序列分析的“通用基础模型”已成为新的研究热点。虽然已有诸如TimesFM、Chronos等探索取得初步进展,但当前模型仍存在上下文理解不充分、泛化能力有限等问题。
在数据层面,不同领域的时序数据存在采样频率差异、噪声水平不同,甚至物理含义各异,建立统一的语义表示亟需深入研究。同时,即使同属一个领域,不同对象(如不同患者或城市)间的时序数据也可能展现出明显的个体差异。此外,不同任务对预测结果的需求各异,模型应具备按需响应和指令适应能力。未来研究亟需探索如何引入文本、图像、图结构等多模态数据,帮助模型更全面地理解和建模复杂的上下文信息。
与此同时,是否存在一个“真正通用”的时间序列基础模型仍是开放问题,也激发了多种探索方向:如基础模型的扩展规律(scaling laws)与能力涌现(emergence)机制研究,不同比例数据对模型能力的影响评估,乃至开发面向特定领域(如医疗、交通等)的定制型基础模型,融合领域知识实现更精准的预测。
6.2 可信时间序列预测:让AI值得信赖
现有大多数预测模型为深度神经网络,虽然具备强大表达能力,但往往难以解释预测原因,不适用于对安全性与可解释性有高要求的场景(如医疗辅助诊断)。未来应当探索将可解释AI(XAI)与因果推理等技术与强预测模型融合,构建“既能预测准,又能说明白”的可信模型。
另一方面,训练跨域模型往往需要汇聚来自多源的数据,如何在提升性能的同时保障用户隐私与系统安全成为关键挑战。当前主流方法多借助联邦学习框架,但如何引入差分隐私等机制来防止数据泄露、如何增强模型抵抗“恶意客户端投毒”等攻击,仍是亟需解决的重要课题,关乎大规模部署可信AI的可行性。
6.3 新型建模范式:从“结构设计”走向“范式革命”
时间序列预测向来是一个开放且包容的研究领域,不同网络结构、训练策略与视角的不断尝试,推动了整体技术生态的演进。近年来,许多前沿机器学习技术也正逐步渗透进时序预测中,带来了新的范式变革机遇。
例如,可探索如何引入AutoML方法,自动调整网络结构、权衡预测精度与计算效率,提升模型在实际部署中的适用性。又如,物理引导神经网络(PINNs)作为一种嵌入先验知识的方式,能够有效应对数据稀缺问题,增强模型的可靠性和可解释性。将这些“跨界”方法与时序预测相融合,预计将为该领域注入新的活力与思维方式。
6.4 全面评估体系:推动模型发展从“跑分”到“认知”
除了模型架构本身,如何科学、公平地评估时序模型的性能也是推动整个领域健康发展的关键。当前主流评估基准普遍面临分布单一、任务难度区分不清的问题,评价指标也多为单一误差指标,难以全面反映模型优势与局限。
这不仅可能引发“跑分竞赛”,更可能掩盖模型在泛化能力、稳定性、计算效率等方面的真实表现。因此,未来需要构建覆盖多分布、多任务、多场景的通用评估数据集,同时引入多元评价维度(如鲁棒性、泛化性、效率等),以促使模型设计更加全面、务实、稳健。
变分自编码器:VAE 通过学习潜在空间中的分布实现重构与生成,可用于概率预测与不确定性建模。TimeVAE 引入时间条件向量,HyVAE 支持多个模态协同生成,广泛用于医疗与金融风险分析。
生成对抗网络:GAN 利用生成器与判别器博弈学习数据分布,适用于生成高质量拟真序列。TimeGAN 结合监督信号保留时间顺序特征,Curb-GAN 在电力与交通场景中展现出良好的数据增强效果。
流模型:流模型通过可逆变换对数据建模,具有明确的密度函数表示,适合概率预测与异常检测。FM-TS 结合频率域结构建模复杂分布,CFMTS 使用耦合变换处理高维序列数据。
扩散模型:扩散模型基于逐步加噪/去噪的过程建模数据生成路径,使得模型能够学习复杂的数据分布并生成高质量的预测,适用于多模态、多样性要求高的场景。TSDiff 通过自我引导提高了短期准确性和数据生成效率;LDT利用潜在扩散模型在降水预报和可扩展性方面都展示了显著的改进。
五、学习范式演进:可迁移、可信的时序预测方法
5.1 自监督学习
对比学习:对比学习通过构造正负样本对,促使模型学习具有判别性的时序表示。在时间序列任务中,对比学习通常结合数据增强策略(如扰动、时间裁剪、遮蔽)以构造多样化的样本视角,从而提升模型在不同场景下的泛化能力。TS2Vec 是时间序列中较早的通用对比学习框架,为无监督特征表示学习奠定了基础。在此基础上,TNC 与 TS-TCC 进一步提升了模型对时间序列中关键特征的提取能力。
掩码自编码器: 掩码自编码器通过有策略地遮蔽部分输入数据,并重建被遮蔽区域,引导模型学习鲁棒的特征表示。在原始数据空间中,TST首次将掩码自编码机制引入时间序列;在离散潜在空间中,TimeMAE与 CrossTimeNet将时间序列映射到统一的离散表示形式,便于跨领域的自监督预训练;SimMTM通过加权聚合相邻时间片的方式重建被遮蔽的时间点,在流行空间中实现了更加结构化的语义建模。
自回归式预训练:自回归模型通过利用历史数据预测未来值,从而捕捉时间序列中的动态变化和时序依赖关系。在时间序列预训练中,自回归机制能够逐步建模序列的演化过程。TimeDART 将时间序列划分为多个数据块,并以 Transformer 编码器建模块间依赖,同时结合扩散与去噪机制,提取块内的细粒度特征,实现了扩散模型在时间序列中的有效应用;Timer 则统一不同类型的时间序列为一种通用格式(S3),并采用 GPT 风格的解码器架构,展现出良好的扩展性与泛化能力。
5.2 领域自适应
由于分布变化(distribution shift)广泛存在于时间序列数据中,导致模型在新领域上预测效果下降,形成典型的“分布外”(OOD)问题。同时,不同领域间序列特征的映射关系往往差异显著,给模型迁移带来额外挑战。因此,提升时间序列预测的可迁移性,核心在于实现有效的领域自适应机制。SLARDA 通过自监督对比预训练,学习更具迁移性的时序表示,同时兼顾时间动态性与特征对齐;FOIL设计替代损失函数与联合优化策略,在存在未观测变量时仍能学习稳定表示,进一步提升 OOD 时间序列的泛化能力。
5.3 基于语言模型的预测方法
近年来,大语言模型(LLMs)因其强大的语义理解与推理能力,被广泛探索用于时间序列预测任务。这类方法可以将时间序列数据转换为类似文本的输入格式,并借助预训练语言模型进行预测。相比传统模型,LLM 更擅长结合结构化信息与文本上下文,如个体特征或采样背景,从而提升预测准确性。
参数调优型方法:通过对预训练模型进行微调,使其更贴合特定时间序列数据。为实现高质量预测,研究者从多个角度提出创新策略。
-
预测方式上,如 AutoTimes 使用自回归(Auto-regressive)方式逐步生成序列,而 FPT 则采用一跳预测(One-step)方式一次性生成完整序列,以减少误差累积。
-
训练范式上,CrossTimeNet 引入自监督预训练,提升模型对时间序列结构的理解。
-
文本融合上,如 TEMPO 结合结构化数据与文本输入,让模型利用自然语言信息辅助预测。
-
参数更新方式上,LLM4TS 采用 LoRA 策略对核心模块低秩微调,也有部分模型直接更新主干参数。
-
输入表示上,Chronos 和 UniTime 采用嵌入后的结构化输入,TimeLLM 则融合时序与文本特征,提升输入信息丰富度。
零调优型方法:该类方法无需修改语言模型参数,直接通过 Prompt 构造完成预测任务,具有部署灵活、成本低等优势。
-
Prompt设计方面,如 LLMTime 将样本背景转为文本信息输入模型,LSTPrompt 引入「思考间歇」机制模拟人类预测过程。
-
上下文增强方面,TimeRAF 采用检索增强生成(RAG)策略,基于相似历史样本构造 Prompt;TimeRAG 将检索样本转化为 JSON 输入,提升推理效果。
-
跨模态理解上,TableTime 验证了 LLaMA 等模型对表格时序数据的理解与分类能力。
-
智能体协作上,TESSA 利用通用与专业注释智能体,提升 GPT-4o 对时间序列的语义解析与推理能力
-
挑战方面,Merrill 等人发现当前零调优模型的预测能力有限,部分任务甚至接近随机水平,表明“时间序列推理”在 LLM 中仍处于早期发展阶段。
5.4 时间序列基座模型构建
近年来,时间序列基础模型在大规模时序数据上预训练后崭露头角,凭借其强大的跨领域泛化能力,正在重塑时间序列预测任务的技术格局。Moirai引入面向任意变量的注意力机制,在大规模 LOTSA 数据集上通过掩码预训练,展现出优异的跨分布预测能力;Timer进一步统一多种预测任务,采用 GPT 式自回归结构,展示出强大的通用预测能力。
尽管结构各异,这些模型都秉持“简洁通用”的设计理念,避免对特定任务的过拟合。当前的发展重点主要集中在:
这些趋势标志着时间序列研究正逐步迈向数据驱动(data-centric)的新范式,在基础模型与下游任务之间建立更稳固的桥梁。
-
构建大规模、跨领域的预训练数据集(如 LOTSA 数据集包含 270 亿时间步);
-
探索统一建模框架以适配多变量分析;
-
利用合成数据提升泛化能力,例如 TimesFM 的训练数据中有 20% 来自合成样本。
5.5 可解释性
可信预测模型不仅要有准确的结果,还应回答“为什么会这么预测”。当前提升预测模型可解释性的主流研究聚焦在两个方向:因果发现(Causal Discovery)和物理引导神经网络(PINNs)。
因果发现方法试图揭示变量之间潜在的因果关系,帮助模型更清晰地识别时间序列中的驱动因素。例如,Granger 因果性分析、动态贝叶斯网络等传统方法为因果推断提供了统计基础,近年来更有融合深度学习的因果建模方式,用于处理非线性与非平稳序列。在复杂系统中,这类方法显著提升了模型的解释能力与泛化性能。
另一方面,PINNs通过将微分方程、守恒定律等物理知识直接嵌入模型结构中,使得预测不仅符合历史数据,也满足自然规律。这种融合物理约束的方式在科学计算、工程建模等领域尤其重要,能够有效应对数据稀疏或噪声干扰,提升模型的可信度和适用性。
5.6 鲁棒性
当前时间序列模型在预测精度上取得了长足进展,但它们对输入扰动仍较敏感,容易受到对抗攻击的干扰,进而产生严重后果。
部分研究提出通过蒙特卡洛估计目标序列分布,生成具有隐蔽性和欺骗性的攻击样本,专门攻击概率型预测模型。针对更具现实性的稀疏攻击场景,学者们发展出如随机平滑与对抗训练等防御机制,在保留模型性能的同时提高鲁棒性。更进一步,像 RDAT 引入强化学习与自蒸馏策略,有效增强了交通预测任务中的防御效果。
此外,BACKTIME 揭示了主流预测模型在面临后门攻击时的脆弱性。这类攻击通过在训练数据中植入稀疏触发器,在预测阶段以极小代价触发错误输出,提示我们必须加强对时序模型安全性的关注与治理。
5.7 隐私保护
大规模预训练已成为时间序列建模的新趋势,但如何在整合多源数据的同时保护用户隐私,成为不可回避的挑战。为此,研究者积极引入联邦学习框架,推动隐私友好的时序预测研究。
例如,CNFGNN 将图结构编码与跨节点联邦学习相结合,在不直接共享数据的前提下建模复杂的空间-时间依赖关系。MetePFL 则引入提示学习机制,并结合图模型减轻多源数据之间的异质性带来的影响。Time-FFM 更进一步构建了融合语言模型与联邦架构的时序基础模型,通过分离全局编码与本地预测模块,在确保隐私的同时保持高度个性化的预测能力。
随着数据合规监管的加强,联邦学习等隐私保护机制将成为可信时序模型发展的重要基石,为实际落地提供可行路径。
六、未来趋势:推动预测从“准”走向“智”
随着时间序列预测在基础模型、可信建模、训练范式等方面不断取得突破,未来的研究将更加多元、深入并面向实际落地,推动预测从“准”走向“智”。
6.1 时间序列基础模型:迈向通用智能的基石
借鉴计算机视觉与自然语言处理领域基础模型的成功经验,构建适用于时间序列分析的“通用基础模型”已成为新的研究热点。虽然已有诸如TimesFM、Chronos等探索取得初步进展,但当前模型仍存在上下文理解不充分、泛化能力有限等问题。
在数据层面,不同领域的时序数据存在采样频率差异、噪声水平不同,甚至物理含义各异,建立统一的语义表示亟需深入研究。同时,即使同属一个领域,不同对象(如不同患者或城市)间的时序数据也可能展现出明显的个体差异。此外,不同任务对预测结果的需求各异,模型应具备按需响应和指令适应能力。未来研究亟需探索如何引入文本、图像、图结构等多模态数据,帮助模型更全面地理解和建模复杂的上下文信息。
与此同时,是否存在一个“真正通用”的时间序列基础模型仍是开放问题,也激发了多种探索方向:如基础模型的扩展规律(scaling laws)与能力涌现(emergence)机制研究,不同比例数据对模型能力的影响评估,乃至开发面向特定领域(如医疗、交通等)的定制型基础模型,融合领域知识实现更精准的预测。
6.2 可信时间序列预测:让AI值得信赖
现有大多数预测模型为深度神经网络,虽然具备强大表达能力,但往往难以解释预测原因,不适用于对安全性与可解释性有高要求的场景(如医疗辅助诊断)。未来应当探索将可解释AI(XAI)与因果推理等技术与强预测模型融合,构建“既能预测准,又能说明白”的可信模型。
另一方面,训练跨域模型往往需要汇聚来自多源的数据,如何在提升性能的同时保障用户隐私与系统安全成为关键挑战。当前主流方法多借助联邦学习框架,但如何引入差分隐私等机制来防止数据泄露、如何增强模型抵抗“恶意客户端投毒”等攻击,仍是亟需解决的重要课题,关乎大规模部署可信AI的可行性。
6.3 新型建模范式:从“结构设计”走向“范式革命”
时间序列预测向来是一个开放且包容的研究领域,不同网络结构、训练策略与视角的不断尝试,推动了整体技术生态的演进。近年来,许多前沿机器学习技术也正逐步渗透进时序预测中,带来了新的范式变革机遇。
例如,可探索如何引入AutoML方法,自动调整网络结构、权衡预测精度与计算效率,提升模型在实际部署中的适用性。又如,物理引导神经网络(PINNs)作为一种嵌入先验知识的方式,能够有效应对数据稀缺问题,增强模型的可靠性和可解释性。将这些“跨界”方法与时序预测相融合,预计将为该领域注入新的活力与思维方式。
6.4 全面评估体系:推动模型发展从“跑分”到“认知”
除了模型架构本身,如何科学、公平地评估时序模型的性能也是推动整个领域健康发展的关键。当前主流评估基准普遍面临分布单一、任务难度区分不清的问题,评价指标也多为单一误差指标,难以全面反映模型优势与局限。
这不仅可能引发“跑分竞赛”,更可能掩盖模型在泛化能力、稳定性、计算效率等方面的真实表现。因此,未来需要构建覆盖多分布、多任务、多场景的通用评估数据集,同时引入多元评价维度(如鲁棒性、泛化性、效率等),以促使模型设计更加全面、务实、稳健。