清华&上海AI Lab提出傅里叶位置编码（FoPE），解决RoPE长文本泛化不足难题。通过傅里叶分析，发现频谱破坏是限制因素。实验表明FoPE显著提升Transformer性能，在AI及其他领域有广泛应用潜力。
原文标题：ICML 2025 | 清华、上海AI Lab等提出傅里叶位置编码，多项任务远超RoPE
原文作者：机器之心
冷月清谈：
怜星夜思：
2、文章中提到“打不过就加入”，FoPE保留了各层中的频谱损坏，转而提出了对于频谱损坏更加鲁棒的位置编码。那么，在其他AI领域，是否有类似“与其对抗不如适应”的策略的成功案例？
3、文章提到FoPE在多个任务上表现超过RoPE，那么，FoPE是否有可能取代RoPE成为新的主流位置编码方式？FoPE的局限性可能是什么？
原文内容
长文本能力对语言模型（LM，Language Model）尤为重要，试想，如果 LM 可以处理无限长度的输入文本，我们可以预先把所有参考资料都喂给 LM，或许 LM 在应对人类的提问时就会变得无所不能。
但是，LM 通常只在较短窗长下进行训练，可能产生过拟合，只学习到指定范围内的位置关系，但是无法理解没学习过的位置关系。为了缓解这个问题，当下最流行的便是引入具有周期性的旋转位置编码（Rotary Position Embedding，RoPE）。由于周期性编码每间隔一定距离就会出现数值重复，所以 LM 可以使用在少数几个周期内学习到的经验泛化到更多的周期当中。
但奇怪的是，使用 RoPE 的 LM 依然难以直接在训练长度之外起效，必须依靠其他算法（如 YARN）来辅助其进行外推。 那么，到底是什么限制了 RoPE 的周期延拓，进而限制了 LM 的长度外推呢？
于是，清华大学讲席教授、上海AI Lab主任/首席科学家周伯文教授的团队对这一问题进行了深入探索，使用傅里叶分析工具解读了使用 RoPE 的 Transformer 模型长文本泛化能力不足的原因之一是 RoPE 带来的周期性延拓受到了频谱破坏的影响。进一步地，该文章提出的傅里叶位置编码（Fourier Position Embedding，FoPE）大幅提升了Transformer的长文本泛化能力。
-
论文标题：Fourier Position Embedding: Enhancing Attention’s Periodic Extension for Length Generalization
-
arXiv 链接：https://arxiv.org/pdf/2412.17739
-
代码链接：https://github.com/TsinghuaC3I/Fourier-Position-Embedding
研究亮点
发现 —— 频谱损坏限制周期延拓
作者们通过观察 RoPE 的公式可以发现，它为 Hidden States 的每一维都指定了单一的频率，并假设这一维度的语义信息按照这个波长影响其他位置的语义。所以，RoPE 周期延拓性的起效前提是 “Hidden States 的每一维只存在单一频率的语义”。如果每一维明明存在不同频率的语义，却仍然按照单一频率的波长来估计这部分语义的传递规律，RoPE 所带来的周期延拓将产生混乱，进而无法实现长文本泛化。
遗憾的是，在使用 RoPE 的 LM 中，这个假设只在 LM 的第一层中成立，但在后面的所有层中都不成立。因为后面的所有层中，每一维中都掺杂了除主频之外的其他频率分量，这个现象可以被称作频谱损坏（Spectrum Damage）。频谱损坏主要有三个来源：① 线性函数；②激活函数；③时域截断。
线性函数
如果我们假设线性层的权重为
，其对输入
进行处理得到输出
，那么每一维输出将由每一维输入的线性组合构成：
考虑到每一维输入所对应的频率是不一样的，那么
将掺杂输入中的所有频率分量。
激活函数
根据高等数学的知识，给定一个含有两个频率的函数
，以及任意一个与时间无关的非线性函数
，
被函数
作用后得到的输出将存在多个频率分量，这些频率将是输入频率的线性组合：
这个结论可以通过泰勒展开进行简单证明，也可以任意地推广到存在更多频率的情况。可以看到，经过线性层之后，每一维本就掺杂了多种频率。在经过激活函数之后，这种掺杂会变得更加严重。
时域截断
给定一个被截断为长度N的单频率函数
通过傅里叶变换可以得到（详见文末）这个函数的频谱是：
其中，
是截断长度与周期长度相除后向下取整，
是在
处无限大但积分为 1、在其他位置取值均为零的奇异函数。可以看到，时域截断会让主要频率
的强度向周围的频率扩散，降低信噪比。如果该函数的周期
大于截断长度N，这个信噪比将变得很低，会极大地抑制对只要频率的学习。巧合的是，RoPE 中其实使用了大量频率低、周期长的分量，所以这个问题尤为严重。
算法 —— 频域鲁棒性是长文本泛化关键
在以往的研究中，大家普遍认为只有 Attention 才会影响长度外推。但从上面的分析可以看出，整个模型中的线性层、激活函数和时域截断也都会对长度外推产生影响，并且是不利影响（也就是上文提到的频谱损坏）。为了改善频谱损坏对长文本泛化的不利影响，这篇论文提出了傅里叶位置编码（FoPE，Fourier Position Embedding）来提升模型的频域鲁棒性和周期延拓性，进而提升长文本泛化。
FoPE 的核心思想是 “打不过就加入”。考虑到线性层和激活函数可以带来更强的表征能力，时域截断又是受到硬件限制无法改变，FoPE 索性就仍然保留了各层中的频谱损坏，转而提出了对于频谱损坏更加鲁棒的位置编码。鲁棒性的提升主要源于两方面：① 既然每一维中不可避免的混杂其他频率的分量，那就干脆在一开始就把每一维都建模成一个傅里叶级数（Fourier Series）。即使这样的建模不会避免频谱破坏，FoPE 却可以在每一维中解码出更多频率的信息（利用三角函数的正交性）；② 既然极低频的分量周期过长，会导致这些频率分量的周期特性无法被学习到，那就将他们裁剪成频率为 0 的直流分量。考虑到直流分量的良好性质（既可以看作周期无限短，又可以看作周期无限长），这个新加入的频率既保证了周期性，又可以让每个词汇的信息向无限远的词汇传递；
综上，FoPE 的公式可以写作：
实验
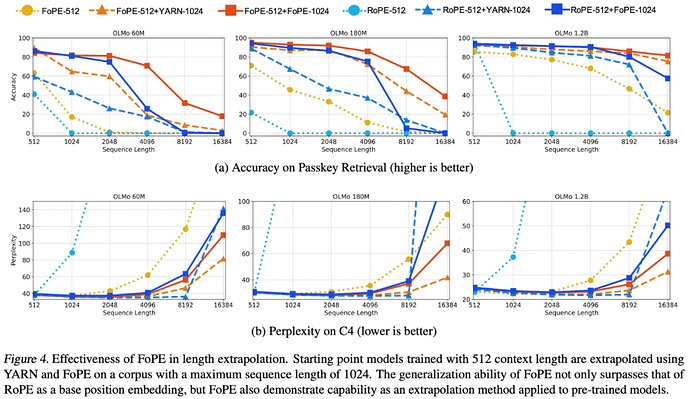
进一步地，文章在困惑度、大海捞针准确率以及很多下游任务 Benchmark 对不同方法进行了对比，实验发现 FoPE 在这些任务上都有稳定的表现，在绝大多数远超过使用 RoPE 的模型。
潜在影响
论文中使用傅里叶工具得到的分析结论和算法可能存在更广泛的潜在价值，有潜力应用在更多的领域和任务：① AI 领域内：长视频生成、kv-cache 压缩、多模型协同等；② AI 领域外：语义通信、光计算和脑机接口。
作者简介：华尔默，清华大学博士生，研究方向是基础模型的架构设计与训练算法设计，在 ICML、ICLR、NeurIPS、ACL、EMNLP、COLM、AAAI 等顶级会议上发表过论文。
© THE END
转载请联系本公众号获得授权
投稿或寻求报道：[email protected]