探索基于Transformer的时间序列去噪技术，模型在不同噪声条件下表现出强大的去噪能力，为后续研究奠定基础。
原文标题：基于Transformer架构的时间序列数据去噪技术研究
原文作者：数据派THU
冷月清谈：
本文深入探讨了如何利用Transformer架构构建时间序列去噪模型。Transformer在自然语言处理领域已取得显著成就，其序列建模能力同样适用于时间序列数据处理。文章首先介绍了时间序列噪声的来源及去噪的重要性，随后详细阐述了基于TensorFlow框架构建Transformer模型的步骤，包括输入嵌入层、位置编码器、Transformer编码器和输出映射层。文章还介绍了如何生成具有特定特性的合成时间序列数据用于模型训练和评估。实验结果表明，该模型在各种噪声条件下均展现出较强的去噪能力，并对注意力机制进行了可视化分析，为特定任务的模型微调和专门化去噪模型的开发提供了基础。
怜星夜思：
1、文章中提到传统去噪方法如移动平均和卡尔曼滤波的局限性，Transformer架构有哪些优势使其在时间序列去噪方面更具潜力？
2、文章中提到位置编码对于Transformer的重要性，如果去除位置编码，模型性能会受到什么影响？在什么类型的时间序列数据中，位置编码可能不那么重要？
3、文章中通过可视化注意力权重矩阵来分析模型的行为，你认为除了注意力权重矩阵，还有哪些方法可以用来解释Transformer在时间序列去噪中的工作原理？
2、文章中提到位置编码对于Transformer的重要性，如果去除位置编码，模型性能会受到什么影响？在什么类型的时间序列数据中，位置编码可能不那么重要？
3、文章中通过可视化注意力权重矩阵来分析模型的行为，你认为除了注意力权重矩阵，还有哪些方法可以用来解释Transformer在时间序列去噪中的工作原理？
原文内容
来源：Deephub Imba本文共6000字，建议阅读15分钟本文将详细探讨一种基于Transformer架构的时间序列去噪模型的构建过程及其应用价值。
Transformer是一种专为处理序列数据而设计的高效神经网络架构。自2017年问世以来，Transformer已在自然语言处理(NLP)领域取得显著成就，并成为现代人工智能平台的核心组件，如OpenAI的ChatGPT[1]、Anthropic的Claude[2]以及Google的Gemini[3]等。除了语言模型应用外，Transformer架构的序列建模能力使其在多种序列数据处理任务中展现出巨大潜力，其中包括本文重点讨论的时间序列去噪应用。
时间序列数据在现实世界中广泛存在，从物理传感器采集的数据(如热敏电阻、加速度计等测量结果)到金融市场的证券价格波动。这些数据通常包含各种来源的噪声干扰，这些噪声可能掩盖了数据中潜在的重要模式和趋势。传统的时间序列去噪方法，如移动平均技术和卡尔曼滤波器[4]等，长期以来一直是处理此类问题的标准工具。
移动平均法虽然实现简单，但由于其固有的平均机制——每个数据点都与其前序点进行平均计算，因此会引入明显的时间滞后，这在需要实时处理的应用场景中可能产生不利影响。
在许多专业领域中，卡尔曼滤波器[4]被视为时间序列去噪的首选技术。卡尔曼滤波器的应用通常需要针对特定监测系统进行复杂且定制化的实现，这增加了其应用难度和适用范围的局限性。
随着深度学习技术的快速发展，特别是Transformer架构的出现，为解决经典的时间序列去噪问题提供了一种新颖且具有潜力的方法。这种基于神经网络的方法有望克服传统技术的局限性，并在复杂的去噪任务中展现出优越性能。
本文将系统性地介绍时间序列去噪问题的理论基础，并详细阐述如何利用TensorFlow框架构建一个在合成数据集上训练的时间序列去噪Transformer模型。
通过对这个精简但功能完整的Transformer模型的深入分析，我们将能够更好地理解经典论文"Attention is All You Need"[5]中提出的核心概念，特别是位置编码(Positional Encoding)和自注意力(Self-Attention)机制的工作原理及其在实际应用中的重要性。
本文所使用的全部源代码已在GitHub仓库[6]开放获取，供读者参考和扩展。
时间序列噪声
时间序列噪声是指序列数据中的非预期波动，这些波动通常会掩盖数据中蕴含的潜在模式和趋势。噪声可能源自多种因素，包括传感器精度不足、环境干扰、市场随机波动或计算过程中的误差累积等。
开发高效的去噪技术对于从时间序列数据中提取有意义的信息、提高传感器测量精度和优化决策过程具有至关重要的意义。
Transformer模型
本文设计的噪声去除Transformer模型由四个主要组件构成：输入嵌入层(Input Embedding Layer)、位置编码器(Positional Encoder)、Transformer编码器(包含全局自注意力层和前馈神经网络)，以及输出映射层。输出映射层负责将Transformer编码器的高维输出转换回原始信号空间，从而生成去噪后的信号。
具体而言，输入嵌入层将长度为1000的噪声输入向量映射到32维的特征空间中。位置编码器则在输入嵌入中为每个元素添加位置信息编码，使模型能够感知序列中元素的相对位置。Transformer编码器通过全局自注意力机制对输入序列中的各个时间步进行分析，从而有效识别并去除噪声成分。最后，模型的输出层将编码器输出从高维特征空间(1000, 32)映射回一维的去噪信号向量(长度为1000)。
接下来，我们将深入探讨Transformer模型的各个关键组件的实现细节和工作原理。
输入嵌入
在Transformer模型中，输入嵌入层的主要作用是将形状为(1000, )的一维噪声时间序列数据映射到形状为(1000, d_model)的高维表示空间，其中d_model = 32表示映射后的特征维度。这一转换过程通过标准的密集神经网络层[7]实现。经过这一处理，原始输入中的每个时间步值都被转换为一个32维的向量表示。
输入嵌入层的输出计算公式如下：
公式中，X表示长度为1000的输入向量，W表示形状为(1000, 32)的可学习权重矩阵，b表示长度为32的偏置向量。经过此层处理后，输出的张量形状为(1000, 32)。
位置编码器
由于Transformer架构本身对输入序列中元素的顺序没有内在感知能力，因此需要通过位置编码器为输入添加位置信息。位置编码器通过计算一组特定的正弦函数值并将其与输入嵌入相加来实现这一功能。位置编码的计算公式如下：
其中，pos表示序列中的位置索引(取值范围为0, 1, ..., 999)，i表示嵌入维度(对于d_model = 32，取值为0, 1, ..., 31)，10000是一个缩放因子，其作用是确保位置编码与输入嵌入的数值量级相近，便于模型学习。
序列长度为1000的32维嵌入的位置编码可视化
位置编码器层的输出是输入嵌入与位置编码的元素级加和：
其中，Length(X) = 1000代表序列长度，d_model = 32代表嵌入空间的维度。
我们Transformer模型中的PositionalEncoding层实现代码如下：
class PositionalEncoding(tf.keras.layers.Layer): def __init__(self, seq_len, d_model, **kwargs): super(PositionalEncoding, self).__init__() self.pos_encoding = self.get_positional_encoding(seq_len, d_model)def get_positional_encoding(self, seq_len, d_model, n=10000):
创建位置数组(形状：[seq_len, 1])
position = np.arange(seq_len)[:, np.newaxis]
创建维度数组(形状：[d_model/2])
denominator = np.power(n, 2 * np.arange(0, d_model, 2) / d_model)
计算正弦函数并堆叠它们
P = np.zeros((seq_len, d_model))
P[:, 0::2] = np.sin(position / denominator) # 对偶数索引应用sin
P[:, 1::2] = np.cos(position / denominator) # 对奇数索引应用cos转换为TensorFlow张量并重塑为(1, seq_len, d_model)
P_tensor = tf.convert_to_tensor(P, dtype=tf.float32)
P_tensor_reshaped = tf.reshape(P_tensor, (1, seq_len, d_model))return P_tensor_reshaped
def call(self, inputs):
return inputs + self.pos_encoding[:, :tf.shape(inputs)[1], :]
Transformer编码器
Transformer编码器构成了噪声去除Transformer模型的核心部分，它由两个主要子层组成：全局自注意力层和前馈神经网络[8]。为了优化模型的训练过程并提高性能，在全局自注意力层和前馈网络之后都应用了残差连接(将层输入直接加到其输出)和层归一化步骤，这有助于缓解梯度消失问题并提高训练稳定性。
全局自注意力[5]层使Transformer能够在处理输入序列时，根据当前生成输出的需要自适应地关注序列中的不同时间步。与循环神经网络(RNN)或卷积神经网络(CNN)不同，全局自注意力机制能够同时处理整个输入序列，从而有效学习全局依赖关系，这对于复杂的时间序列去噪任务尤为重要。
本模型使用TensorFlow提供的MultiHeadAttention[9]层来实现自注意力计算。具体计算过程如下：
首先，全局自注意力层将形状为(1000, 32)的位置编码器输出X作为输入，分别生成查询矩阵Q、键矩阵K和值矩阵V：
其中，W_Q、W_K和W_V是形状为(1000, dₖ)的可学习权重矩阵。在单头注意力的情况下，dₖ = d_model/H，其中H = 1是注意力头的数量，因此对于本模型，dₖ = 32。
接下来，通过计算查询矩阵Q与键矩阵K的转置之间的点积，得到注意力分数：
这个注意力分数是一个形状为(1000, 1000)的矩阵，其中每个元素表示输入序列中一个时间步对另一个时间步的关注程度。
然后，对注意力分数进行缩放并应用softmax函数，以稳定训练过程并获得概率化的注意力分布，确保注意力权重矩阵的每一行元素和为1：
最后，通过对形状为(1000, 1000)的注意力权重矩阵与形状为(1000, 32)的值矩阵V进行点积运算，计算得到全局自注意力层的输出，其形状为(1000, 32)：
全局自注意力层GlobalSelfAttention层的具体实现代码如下：
class BaseAttention(tf.keras.layers.Layer): def __init__(self, **kwargs): super().__init__() self.mha = tf.keras.layers.MultiHeadAttention(**kwargs) self.add = tf.keras.layers.Add() self.layernorm = tf.keras.layers.LayerNormalization()
class GlobalSelfAttention(BaseAttention):
def call(self, x):
attn_output, attn_scores = self.mha(
query=x,
value=x,
key=x,
return_attention_scores=True)
x = self.add([x, attn_output])
x = self.layernorm(x)
return x, attn_scores
值得注意的是，GlobalSelfAttention类继承自BaseAttention基类。这种设计模式使得我们可以基于相同的基础结构实现不同类型的注意力机制，例如，我们可以轻松实现一个CausalSelfAttention层：
class CausalSelfAttention(BaseAttention): def call(self, x): attn_output, attn_scores = self.mha( query=x, value=x, key=x, return_attention_scores=True, use_causal_mask = True) x = self.add([x, attn_output]) x = self.layernorm(x) return x, attn_scores
CausalSelfAttention类与GlobalSelfAttention类的主要区别在于它启用了因果掩码(Causal Mask)，即将未来时间步的注意力权重设置为0。因果自注意力确保序列中某个位置的输出仅基于该位置及其之前位置的信息，这种机制在文本生成等需要逐步预测的任务中尤为重要。
Transformer编码器中的前馈网络[8]由两个大小分别为128和32的密集层[7]组成，同时集成了一个dropout层[10]以防止模型过拟合。前馈网络在全局自注意力层混合各时间步信息后，对每个时间步独立进行处理，进一步增强了模型的表达能力。
前馈网络的数学表达如下：
其中，W₁和W₂分别是大小为(32, d_ff)和(d_ff, 32)的可学习权重矩阵(前馈网络的维度d_ff = 128)，b₁和b₂分别是长度为d_ff和32的偏置向量。经过处理后，前馈网络输出的张量形状为(1000, 32)。
FeedForward层的实现代码如下：
class FeedForward(tf.keras.layers.Layer): def __init__(self, d_model, dff, dropout_rate=0.1): # dff = 前馈网络的维度（隐藏层的大小） super().__init__() self.seq = tf.keras.Sequential([ tf.keras.layers.Dense(dff, activation='relu'), tf.keras.layers.Dense(d_model), tf.keras.layers.Dropout(dropout_rate) ]) self.add = tf.keras.layers.Add() self.layer_norm = tf.keras.layers.LayerNormalization()
def call(self, x):
x = self.add([x, self.seq(x)])
x = self.layer_norm(x)
return x
在全局自注意力层和前馈网络之后应用的残差连接和层归一化步骤可表示为：
完整的EncoderLayer实现代码如下：
class EncoderLayer(tf.keras.layers.Layer): def __init__(self,*, d_model, num_heads, dff, dropout_rate=0.1): super().__init__()self.self_attention = GlobalSelfAttention(
num_heads=num_heads,
key_dim=d_model,
dropout=dropout_rate)self.ffn = FeedForward(d_model, dff)
def call(self, x):
x, attn_scores = self.self_attention(x)
x = self.ffn(x)
return x, attn_scores
输出映射层
Transformer编码器输出的张量形状为(1000, 32)。模型的最终输出层负责将这个高维特征表示映射回原始信号空间，生成形状为(1000, )的去噪信号向量。这一映射过程通过单个密集层[7]实现。
完整的NoiseRemovalTransformer模型实现代码如下：
class NoiseRemovalTransformer(tf.keras.Model): def __init__(self, d_model, seq_len, num_heads, dff, num_layers, dropout_rate=0.1): super(NoiseRemovalTransformer, self).__init__() # 嵌入层 self.embedding_layer = tf.keras.layers.Dense(d_model, activation=None)位置编码层
self.pos_encoding_layer = PositionalEncoding(seq_len, d_model)
编码器层
self.enc_layers = [EncoderLayer(d_model=d_model, num_heads=num_heads, dff=dff, dropout_rate=dropout_rate)
for _ in range(num_layers)]最终层
self.final_layer = tf.keras.layers.Dense(1, activation=None) # 为每个时间步输出单个值
def call(self, x, return_attn_scores=False):
x = self.embedding_layer(x)x = self.pos_encoding_layer(x)
for i in range(len(self.enc_layers)):
x, attn_scores = self.enc_layersix = self.final_layer(x)
if return_attn_scores:
return x, attn_scores
return x
生成合成时间序列数据
为了训练模型，我们生成了具有特定特性的合成时间序列数据。数据生成过程分为三个关键步骤：
首先，使用随机游走算法[11]生成干净的基础信号。为了使生成的信号更加平滑并适合模型训练，我们对随机游走的输出进行平滑处理，并将其缩放至[-1, 1]范围内。
其次，为每个干净信号生成对应的噪声配置文件。这一过程首先为基础噪声水平指定一个随机值(0.1到0.5之间)，然后通过将基础噪声乘以一个可变的噪声因子(0.5到2之间)计算最大和最小噪声水平。最后，通过在最大和最小噪声水平之间均匀采样并进行插值，生成完整的噪声配置文件。
噪声信号通过将干净信号与生成的噪声配置文件相加得到：
其中，f(t)C表示干净信号，f(t)N表示噪声信号，μ(t)表示噪声配置文件。
最后，为了准备训练数据，对噪声信号f(t)N_应用缩放，使其在[-1, 1]范围内。相同的缩放系数也应用于干净信号，以确保正确配对的信号对：
模型训练
模型在由1000个生成的信号对组成的数据集上进行训练，其中800个样本用于训练集，200个样本用于验证集。训练过程使用Adam优化器[12]，学习率设置为0.001。损失函数选用均方误差(MSE)，同时在训练过程中监控平均绝对误差(MAE)指标。训练数据以16个样本为一批(batch)进行处理，总共进行100个训练周期(epochs)。
实验结果
经过训练，噪声去除Transformer模型在验证集上收敛至MSE = 0.0026和MAE = 0.0387的性能水平。
训练历史图表(左：MSE损失函数变化曲线，右：MAE评估指标变化曲线)
信噪比与模型性能关系
考虑到每个样本具有不同的噪声配置文件，我们可以通过分析模型在不同噪声条件下的表现来深入了解其性能特性。为此，我们绘制了模型MSE与原始干净信号和噪声信号间信噪比(SNR)的散点图。SNR(以分贝为单位)的计算公式为：
SNR是衡量信号质量的重要指标，表示干净信号相对于噪声的强度。较高的SNR值表示较好的信号质量，而较低的SNR值则表示较差的信号质量。当SNR小于0时，意味着噪声强度超过了信号强度。
MSE与SNR的关系散点图
上图展示了500个训练样本的散点分布，可以观察到大多数样本集中在MSE = 0.002和SNR = 5 dB附近。
在图中可以观察到两个特殊区域：min(SNR)（对应低MSE）区域和max(MSE)（对应高SNR）区域。这两个区域的样本表现出与直觉预期相反的情况，即低SNR对应低MSE，而高SNR对应高MSE。
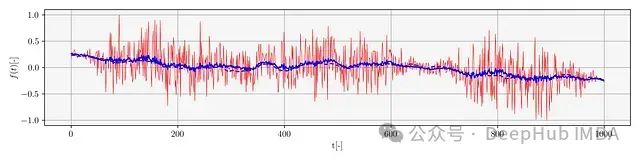
以下是这两个特殊区域以及主样本簇中典型样本的可视化结果。在每个图中，模型输出的去噪信号用蓝色实线表示，原始干净信号用蓝色虚线表示，噪声信号(模型输入)用红色实线表示。
最小SNR样本(SNR = -7.047，MSE = 0.002)
最大MSE样本(SNR = 8.727，MSE = 0.011)
主样本簇中的典型样本(SNR = 5.709，MSE = 0.002)
注意力机制内部分析
通过可视化注意力权重矩阵，我们可以深入了解噪声去除Transformer中全局自注意力机制的工作原理。在注意力权重矩阵中，行对应查询位置(从序列中收集信息的位置)，列对应键位置(被查看信息的序列位置)。
下图展示了主样本簇中典型样本的注意力权重分布：
主样本簇中典型样本的注意力权重矩阵(SNR = 5.709，MSE = 0.002)
结果讨论
通过实验结果分析，我们发现噪声去除Transformer模型在各种噪声条件下展示出了较强的去噪能力。结果部分中展示的三个代表性样本揭示了模型在不同场景下的性能特点。
在min(SNR)样本(对应低MSE)中，虽然噪声水平较高(SNR为负值)，但由于原始干净信号的波动较小，模型能够较好地重建信号特征，从而实现低MSE。
而在max(MSE)样本(对应高SNR)中，尽管噪声水平相对较低，但原始干净信号呈现强烈的波动特性，使得模型难以准确重建其中的高频细节，导致较高的MSE值。
主样本簇中的典型样本(MSE = 0.002，SNR = 5 dB)代表了模型在中等噪声条件和适中信号波动情况下的表现，模型能够有效地去除噪声并重建原始信号。
从主样本簇中典型样本的注意力权重矩阵可以观察到明显的对角线优势，表明在进行去噪处理时，模型主要关注当前时间步及其邻近时间步的信息。此外，注意力权重矩阵中存在多条对角线带，这表明模型已经学习到训练数据中的某些周期性结构，这可能是由于合成数据生成方法导致的。
本研究中的模型是在具有不同噪声水平和整体较低SNR的样本上进行训练的。未来的研究方向可以包括针对特定噪声特征的模型微调，以及为特定去噪任务开发专门化的Transformer模型。通过生成具有系统特定噪声配置文件的合成训练数据，我们可以训练适应各种具体应用场景的专业去噪模型。
总结
本文提出了一种基于Transformer架构的时间序列去噪模型，系统介绍了时间序列去噪问题的理论基础，并详细阐述了一个能够接受噪声输入信号并输出去噪信号的小型Transformer模型的构建过程。为了训练和评估模型，我们生成了具有特定特性的合成时间序列数据。
实验结果表明，所提出的噪声去除Transformer模型在各种噪声条件下均展现出了较强的去噪能力。本文介绍的基础Transformer架构为特定任务的模型微调和专门化去噪模型的开发提供了坚实的基础。
编辑：王菁
