深入解析18种强化学习算法,包括SAC、TRPO、DQN、MADDPG等,助你掌握从基础到高级的RL技术,并提供实战代码参考。
原文标题:18个常用的强化学习算法整理:从基础方法到高级模型的理论技术与代码实现(下)
原文作者:数据派THU
冷月清谈:
怜星夜思:
2、TRPO算法通过KL散度约束策略更新的幅度,为何要约束这个幅度?如果更新幅度过大,可能会导致什么问题?
3、DQN算法中,经验回放机制是如何打破数据相关性的?除了经验回放,还有没有其他方法来解决数据相关性问题?
原文内容
来源:Deephub Imba本文共17000字,建议阅读20分钟本文系统讲解从基本强化学习方法到高级技术(如PPO、A3C、PlaNet等)的实现原理与编码过程,旨在通过理论结合代码的方式,构建对强化学习算法的全面理解。
11、SAC (最大熵演员-评论家算法)
-
评论家网络更新: SAC采用特殊的Q值目标计算方法。系统使用目标网络获取对从当前策略(在下一状态s'评估)采样的下一动作(a')的最小Q值估计(Min Q')。
-
随后从该最小Q值中减去**熵项(α * log π(a'|s'))以获得"软目标值"。TD目标(y)由即时奖励和此软目标组合而成。主评论家网络(Q_ϕ,通常是双Q网络Q1, Q2)通过最小化与y之间的MSE损失**进行参数更新。
-
演员网络更新: 演员网络**为批次状态s采样动作(a_π)。损失函数设计鼓励产生高Q值(由主评论家评估)且同时具有高熵(高log π)的动作分布**。损失函数近似为:
(α * log π − min(Q1, Q2)).mean()
-
Alpha自动调节(可选): 熵温度参数(α)可通过自动调节机制优化,方法是设定目标熵水平并调整α以促使**策略实际熵接近目标值**。
-
目标网络更新: 目标评论家网络通过软更新机制逐步更新。SAC通常不使用目标演员网络,而是使用当前演员网络进行目标动作采样。
-
最大熵框架: 将策略熵H(π(⋅∣s))_H_(_π_(⋅∣ _s_))作为奖励的补充项,在标准奖励基础上添加熵奖励。
-
随机演员设计: 输出连续动作概率分布(如高斯分布)参数(均值、标准差),并从中采样具体动作。
-
双Q网络机制: 使用两个独立Q网络并取其目标值的最小值,以抑制Q值过估计问题(类似TD3)。
-
熵温度系数: 控制奖励目标与熵目标间的平衡权重。可设为固定值或通过自动调整机制优化。
LOG_STD_MAX = 2 LOG_STD_MIN = -20 EPSILON = 1e-6 # 用于log_prob计算中的数值稳定性class ActorNetworkSAC(nn.Module):
“”" SAC的随机高斯演员。“”"
def init(self, state_dim: int, action_dim: int, max_action: float):
super(ActorNetworkSAC, self).init()
self.layer1 = nn.Linear(state_dim, 256)
self.layer2 = nn.Linear(256, 256)
self.mean_layer = nn.Linear(256, action_dim) # 输出均值
self.log_std_layer = nn.Linear(256, action_dim) # 输出对数标准差
self.max_action = max_actiondef forward(self, state: torch.Tensor) -> Tuple[torch.Tensor, torch.Tensor]:
“”" 输出压缩后的动作及其对数概率。“”"
x = F.relu(self.layer1(state))
x = F.relu(self.layer2(x))
mean = self.mean_layer(x)
log_std = self.log_std_layer(x)
log_std = torch.clamp(log_std, LOG_STD_MIN, LOG_STD_MAX) # 为稳定性而夹紧
std = torch.exp(log_std)创建分布并使用重参数化技巧采样
normal_dist = Normal(mean, std)
z = normal_dist.rsample() # 可微分样本(压缩前)
action_squashed = torch.tanh(z) # 应用tanh压缩计算log_prob并修正tanh
log_prob = log_normal(z) - log(1 - tanh(z)^2 + eps)
log_prob = normal_dist.log_prob(z) - torch.log(1 - action_squashed.pow(2) + EPSILON)
在动作维度上对log_prob求和(如果action_dim > 1)
log_prob = log_prob.sum(dim=-1, keepdim=True)
将动作缩放至环境边界
action_scaled = action_squashed * self.max_action
return action_scaled, log_prob
# SAC的评论家网络(双Q) class CriticNetworkSAC(nn.Module): def __init__(self, state_dim: int, action_dim: int): super(CriticNetworkSAC, self).__init__() # Q1架构 self.l1_q1 = nn.Linear(state_dim + action_dim, 256) self.l2_q1 = nn.Linear(256, 256) self.l3_q1 = nn.Linear(256, 1) # Q2架构 self.l1_q2 = nn.Linear(state_dim + action_dim, 256) self.l2_q2 = nn.Linear(256, 256) self.l3_q2 = nn.Linear(256, 1)def forward(self, state: torch.Tensor, action: torch.Tensor) -> Tuple[torch.Tensor, torch.Tensor]:
sa = torch.cat([state, action], 1)
q1 = F.relu(self.l1_q1(sa))
q1 = F.relu(self.l2_q1(q1))
q1 = self.l3_q1(q1)
q2 = F.relu(self.l1_q2(sa))
q2 = F.relu(self.l2_q2(q2))
q2 = self.l3_q2(q2)
return q1, q2
-
奖励曲线: SAC展示出优异的学习效率,累积奖励从初始约-1500迅速提升,并在大约40-50回合后稳定在约-200水平。收敛后的性能表现相对稳定,波动较小。
-
评论家学习: 平均评论家损失在初期显著上升,随后在一定波动范围内趋于稳定,类似于DDPG的模式,反映了随着演员策略改进,评论家需要不断适应更高价值的状态-动作评估。
-
演员学习: 演员损失曲线呈现先增后减的趋势,初期快速上升(表明策略成功更新朝向更高Q值方向),在约40回合达到峰值,之后逐渐下降,这可能反映了策略稳定性提高和熵正则化效应的平衡。
-
熵温度调节: 熵温度参数(Alpha)展示了动态调整过程,初期减小,在主要学习阶段(20-55回合)显著增加,随后再次降低,这与策略从初始探索逐渐转向利用阶段的预期行为一致。Alpha损失在零附近的波动确认了自动调整机制的有效运行,成功维持了目标熵水平。
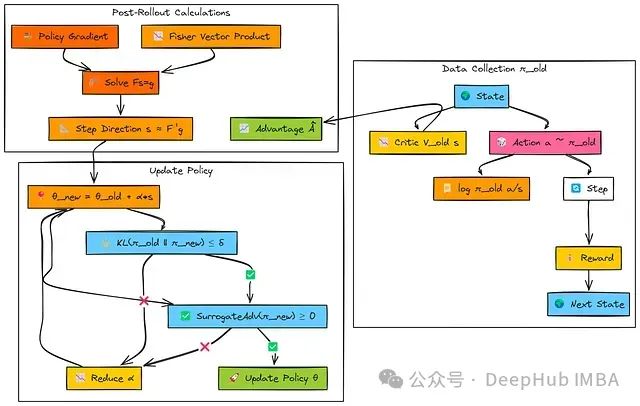
12、TRPO (约束策略更新)
-
信任区域约束: 将策略更新限制在性能改进近似有效的区域内,确保学习过程的稳定性。
-
KL散度约束: 使用平均Kullback-Leibler散度DKL(πold∣∣πnew)≤δ _DKL_ (_πold_ ∣∣ _πnew_ )≤ _δ_作为策略变化的度量标准。
-
Fisher信息矩阵(FIM): 表征策略分布空间的局部曲率特性。TRPO通过涉及FIM的二次形式来近似KL约束。
-
Fisher-向量积(FVP): 一种利用自动微分高效计算FIM与任意向量乘积的技术,避免了构建和存储完整FIM的计算开销。
-
共轭梯度(CG)算法: 一种迭代求解线性系统Fs≈g的方法,用于高效计算更新方向。
-
线搜索机制: 确保最终采用的更新步长满足KL约束,并根据替代目标函数改进性能。
# 使用Hessian-向量积近似计算Fisher向量积 # 这用于共轭梯度方法,计算TRPO更新步骤中的搜索方向 def fisher_vector_product(actor, states, vector, cg_damping): log_probs = actor.get_log_probs(states).detach() kl = (log_probs.exp() * (log_probs - log_probs.detach())).sum() grads = torch.autograd.grad(kl, actor.parameters(), create_graph=True) flat_grads = torch.cat([g.view(-1) for g in grads])gv = torch.dot(flat_grads, vector)
hv = torch.autograd.grad(gv, actor.parameters())
flat_hv = torch.cat([h.view(-1) for h in hv])添加阻尼项以提高数值稳定性
return flat_hv + cg_damping * vector
实现共轭梯度方法解Ax = b
这用于近似TRPO更新步骤中的自然梯度方向
def conjugate_gradient(fvp_func, b, cg_iters=10, tol=1e-10):
x = torch.zeros_like(b) # 初始化解向量
r = b.clone() # 残差
p = b.clone() # 搜索方向
rs_old = torch.dot(r, r)for _ in range(cg_iters):
Ap = fvp_func(p)
alpha = rs_old / torch.dot(p, Ap)
x += alpha * p
r -= alpha * Ap
rs_new = torch.dot(r, r)if rs_new < tol:
breakp = r + (rs_new / rs_old) * p
rs_old = rs_newreturn x
执行回溯线搜索以找到可接受的步长
确保满足KL散度约束
且新策略改进了替代损失
def backtracking_line_search(actor, states, actions, advantages, old_log_probs,
step_direction, initial_step_size, max_kl, decay=0.8, max_iters=10):
theta_old = {name: param.clone() for name, param in actor.named_parameters()} # 存储旧参数for i in range(max_iters):
step_size = initial_step_size * (decay ** i) # 渐进减小步长将步骤应用于演员参数
for param, step in zip(actor.parameters(), step_size * step_direction):
param.data.add_(step)计算KL散度和替代损失
kl = actor.kl_divergence(states, old_log_probs)
surrogate = actor.surrogate_loss(states, actions, advantages, old_log_probs)检查KL是否在约束内且替代损失是否有改善
if kl <= max_kl and surrogate >= 0:
return step_size * step_direction, True如果步骤不成功,恢复旧参数
for name, param in actor.named_parameters():
param.data.copy_(theta_old[name])return None, False # 如果找不到有效步骤,返回失败
使用TRPO算法更新演员(策略)和评论家(价值函数)
def update_trpo(actor, critic, actor_optimizer, critic_optimizer,
states, actions, advantages, returns_to_go, log_probs_old,
max_kl=0.01, cg_iters=10, cg_damping=0.1, line_search_decay=0.8,
value_loss_coeff=0.5, entropy_coeff=0.01):计算策略梯度
policy_loss = actor.surrogate_loss(states, actions, advantages, log_probs_old)
grads = torch.autograd.grad(policy_loss, actor.parameters())
g = torch.cat([grad.view(-1) for grad in grads])使用共轭梯度计算自然梯度方向
fvp_func = lambda v: fisher_vector_product(actor, states, v, cg_damping)
step_direction = conjugate_gradient(fvp_func, g, cg_iters)基于KL约束计算步长
sAs = torch.dot(step_direction, fvp_func(step_direction))
step_size = torch.sqrt(2 * max_kl / (sAs + 1e-8))执行回溯线搜索以确保满足KL约束
step, success = backtracking_line_search(actor, states, actions, advantages, log_probs_old,
step_direction, step_size, max_kl, line_search_decay)如果成功,应用步骤
if success:
with torch.no_grad():
for param, step_val in zip(actor.parameters(), step):
param.data.add_(step_val)计算并更新价值函数,使用MSE损失
value_loss = nn.MSELoss()(critic(states), returns_to_go)
critic_optimizer.zero_grad()
value_loss.backward()
critic_optimizer.step()
return policy_loss.item(), value_loss.item() # 返回损失值,用于监控
-
学习效率与性能: TRPO展示出极高的样本效率;平均奖励在仅约20-30次迭代内迅速攀升至接近最优水平,并保持稳定。平均回合长度同样呈现快速下降趋势,迅速稳定在较低水平。
-
评论家学习稳定性: 评论家损失在初期波动后相对迅速地趋于稳定,表明价值函数学习过程高效且一致。
-
策略更新约束(KL散度): "实际KL散度"图显示每次迭代的策略变化量。TRPO设计目标是将这一变化量维持在较小范围内(低于红线所示Max KL阈值,通常约0.01)以确保更新稳定性。图中显示的值呈现异常(部分为负值,理论上KL散度不应为负),但算法的设计意图是实现稳定、约束的更新。
-
优化目标进展: "替代目标"图显示TRPO在采取更新步骤前计算的预期性能改进。曲线在零附近的波动表明逐步改进保证并非总是完美满足,但整体算法表现出色。
13、DQN (深度Q学习)
-
一个神经网络结构(如多层感知机MLP或卷积神经网络CNN),用于近似Q(s, a)函数。该网络通常接收状态s作为输入,输出所有可能离散动作的Q值。
-
一个用于存储历史交互数据(s, a, r, s', done)的经验缓冲区。通过采样随机小批量数据,有效打破了时序相关性,提高了学习过程的稳定性和效率。
-
Q网络的独立副本,其参数(θ⁻)更新频率较低(例如,每C步更新一次或通过慢速"软"更新机制)。这为学习过程提供了稳定的目标值:

# DQN网络(MLP) class DQN(nn.Module): def __init__(self, n_observations: int, n_actions: int): super(DQN, self).__init__() self.layer1 = nn.Linear(n_observations, 128) self.layer2 = nn.Linear(128, 128) self.layer3 = nn.Linear(128, n_actions) # 输出每个动作的Q值def forward(self, x: torch.Tensor) -> torch.Tensor:
“”" 前向传递获取Q值。“”"确保输入是正确设备上的浮点张量
if not isinstance(x, torch.Tensor):
x = torch.tensor(x, dtype=torch.float32, device=x.device)
elif x.dtype != torch.float32:
x = x.to(dtype=torch.float32)
x = F.relu(self.layer1(x))
x = F.relu(self.layer2(x))
return self.layer3(x) # 原始Q值
# 用于存储转换的结构 Transition = namedtuple('Transition', ('state', 'action', 'next_state', 'reward', 'done'))经验回放缓冲区
class ReplayMemory:
def init(self, capacity: int):
self.memory = deque(, maxlen=capacity)def push(self, *args: Any) -> None:
“”" 保存一个转换元组(s, a, s’, r, done)。“”"确保张量存储在CPU上,避免GPU内存问题
processed_args =
for arg in args:
if isinstance(arg, torch.Tensor):
processed_args.append(arg.cpu())
elif isinstance(arg, bool): # 将done标志作为张量存储以保持一致性
processed_args.append(torch.tensor([arg], dtype=torch.bool))
else:
processed_args.append(arg)self.memory.append(Transition(*processed_args))
•
• def sample(self, batch_size: int) -> Optional[List[Transition]]:
• “”" 采样一个随机转换批次。“”"
• if len(self.memory) < batch_size:
• return None
• return random.sample(self.memory, batch_size)
•
def len(self) -> int:
return len(self.memory)
# 动作选择(使用DQN的Epsilon-Greedy) def select_action_dqn(state: torch.Tensor, policy_net: nn.Module, epsilon: float, n_actions: int, device: torch.device) -> torch.Tensor: """ 使用策略Q网络以epsilon-greedy方式选择动作。""" if random.random() < epsilon: # 探索:选择一个随机动作 action = torch.tensor([[random.randrange(n_actions)]], device=device, dtype=torch.long) else: # 利用:根据Q网络选择最佳动作 with torch.no_grad(): # 如果需要,添加批次维度,确保张量在正确设备上 state = state.unsqueeze(0) if state.dim() == 1 else state state = state.to(device) # 获取Q值并选择具有最大Q的动作 action = policy_net(state).max(1)[1].view(1, 1) return action
# DQN优化步骤概述 def optimize_model_dqn(memory: ReplayMemory, policy_net: DQN, target_net: DQN, optimizer: optim.Optimizer, batch_size: int, gamma: float, device: torch.device): """ 对DQN策略网络执行一步优化。""" # 1. 从内存中采样批次 # 2. 准备批次张量(states, actions, rewards, next_states, dones)在'device'上 # 3. 使用policy_net计算所采取动作的Q(s_t, a_t) state_action_values = policy_net(state_batch).gather(1, action_batch) # 4. 使用target_net计算V(s_{t+1}) = max_{a'} Q(s_{t+1}, a'; θ⁻) with torch.no_grad(): next_state_values = target_net(non_final_next_states).max(1)[0] # 5. 计算TD目标y = reward + gamma * V(s_{t+1}) (处理终止状态) expected_state_action_values = (next_state_values * gamma) + reward_batch # 6. 计算Q(s_t, a_t)和TD目标y之间的损失(例如,Huber损失) loss = F.smooth_l1_loss(state_action_values, expected_state_action_values.unsqueeze(1)) # 7. 优化policy_net optimizer.zero_grad() loss.backward() torch.nn.utils.clip_grad_value_(policy_net.parameters(), 100) # 可选梯度裁剪 optimizer.step()完整实现见13_dqn.ipynb
-
学习进展: DQN展示了明显的学习效果。平均奖励值从初始的负值显著增长,在大约200-250回合后趋于稳定,达到持续性的正向奖励水平。
-
训练效率: 回合长度随训练进程显著减少,与奖励增长趋势相一致,表明智能体逐步掌握了更高效地到达目标的能力。
-
探索机制: epsilon衰减曲线显示了探索行为的逐步减少过程,使智能体能够在后期训练阶段更有效地利用已习得的知识。
-
策略学习效果: 最终学习得到的策略网格展示了一个结构合理的决策方案,动作选择通常引导智能体朝向目标状态'G'(位于网格右下角)。
14、MADDPG (多智能体深度确定性策略梯度)
-
Critic更新(智能体i): 智能体i的Critic网络(Q_ϕi)基于目标值进行参数更新。该目标值计算依赖于:智能体i的即时奖励(r_i);目标集中式Critic(Q_ϕi′)的输出,该Critic接收以下输入:联合后续观察状态以及所有目标Actor网络(μ_θj′(o_j′))预测的后续动作
-
智能体i的Actor网络(μ_θi)参数更新目标是生成能够最大化其主集中式Critic(Q_ϕi)估计的Q值的动作,同时考虑所有Actor网络当前预测的动作分布。
-
所有目标网络通过从对应主网络进行缓慢的软更新来更新参数。
-
分散式Actor架构: 每个智能体i拥有独立的策略网络μ_i(o_i),该网络仅使用智能体局部观察o_i来选择动作a_i。
-
集中式Critic架构: 每个智能体i配备对应的Critic网络Q_i(x, a_1, ..., a_N),该网络以联合状态/观察x和所有智能体的动作(a_1, ..., a_N)作为输入,用于估计智能体i的价值函数。
-
离策略学习: 算法使用存储联合交互数据的回放缓冲区,支持从历史经验中进行高效学习。
# Actor网络(类似于DDPG的,每个智能体一个) class ActorNetworkMADDPG(nn.Module): def __init__(self, obs_dim: int, action_dim: int, max_action: float): super(ActorNetworkMADDPG, self).__init__() self.layer1 = nn.Linear(obs_dim, 128) self.layer2 = nn.Linear(128, 128) self.layer3 = nn.Linear(128, action_dim) self.max_action = max_action
def forward(self, obs: torch.Tensor) -> torch.Tensor:
x = F.relu(self.layer1(obs))
x = F.relu(self.layer2(x))
action = self.max_action * torch.tanh(self.layer3(x)) # 缩放的连续动作
return action
# 集中式Critic网络(每个智能体一个) class CentralizedCriticMADDPG(nn.Module): def __init__(self, joint_obs_dim: int, joint_action_dim: int): super(CentralizedCriticMADDPG, self).__init__() # 输入大小 = 所有观察的组合维度 + 所有动作 self.layer1 = nn.Linear(joint_obs_dim + joint_action_dim, 256) self.layer2 = nn.Linear(256, 256) self.layer3 = nn.Linear(256, 1) # 输出该智能体的单一Q值def forward(self, joint_obs: torch.Tensor, joint_actions: torch.Tensor) -> torch.Tensor:
连接所有观察和所有动作
x = torch.cat([joint_obs, joint_actions], dim=1)
x = F.relu(self.layer1(x))
x = F.relu(self.layer2(x))
q_value = self.layer3(x)
return q_value
# --- MADDPG更新逻辑概述(对于智能体i) --- # 假设已处理优化器、目标网络、批次采样1. 从缓冲区中采样联合转换批次:
batch_obs, batch_actions, batch_rewards, batch_next_obs, batch_dones
— Critic_i更新 —
with torch.no_grad():
target_next_actions = [target_actor_j(batch_next_obs_j) for j in range(num_agents)]
target_next_actions_cat = torch.cat(target_next_actions, dim=1)
joint_next_obs_cat = batch_next_obs.view(batch_size, -1)
q_target_next = target_critic_i(joint_next_obs_cat, target_next_actions_cat)
td_target_i = batch_rewards_i + gamma * (1 - batch_dones_i) * q_target_nextjoint_obs_cat = batch_obs.view(batch_size, -1)
joint_actions_cat = batch_actions.view(batch_size, -1)
q_current_i = critic_i(joint_obs_cat, joint_actions_cat)critic_loss_i = F.mse_loss(q_current_i, td_target_i.detach())
优化critic_i
— Actor_i更新 —
冻结critic梯度
current_actions = [actor_j(batch_obs_j) for j in range(num_agents)]
current_actions[i] = actor_i(batch_obs_i)
current_actions_cat = torch.cat(current_actions, dim=1)actor_loss_i = -critic_i(joint_obs_cat, current_actions_cat).mean()
优化actor_i
解冻critic梯度
— 软更新目标网络 —
soft_update(target_critic_i, critic_i, tau)
soft_update(target_actor_i, actor_i, tau)
-
奖励表现(共享): 每回合总共享奖励呈现显著波动,其移动平均线仅显示微弱的上升趋势,最终在一个相对较低的水平(约-50)趋于平稳。这表明智能体在学习过程中取得一定进展,但在200回合的训练周期内未能收敛至高效的合作策略。
-
Critic网络表现: 平均Critic损失值快速下降并稳定在较低水平,表明Critic网络在预测当前智能体策略组合下的价值函数方面逐渐变得准确。
-
Actor网络表现: 平均Actor损失(策略梯度)持续减小(朝负方向增大),表明Actor网络从对应Critic接收到一致的优化信号,策略更新方向符合预期。
15、QMIX (协作型价值分解方法)
-
对于每个智能体i,目标网络Q_i'(θ_i')用于确定从后续观察o_i'出发的最优动作对应的Q值。
-
这些个体最大Q值被输入到目标混合网络``f_mix'(ϕ_mix')中,该网络同时接收后续全局状态x'作为输入,综合生成目标联合价值Q_tot'。
-
系统计算标准TD目标y:y = r + γQ_tot'。
-
对于每个智能体i,主网络Q_i(θ_i)计算在当前批次数据中实际执行的动作a_i对应的Q值。
-
这些Q值与当前全局状态x一起输入到主混合网络``f_mix(ϕ_mix)中,生成当前联合价值估计Q_tot。
-
系统计算y与Q_tot之间的均方误差损失。
# 智能体网络(类似于DQN的Q网络) class AgentQNetwork(nn.Module): def __init__(self, obs_dim: int, action_dim: int): super(AgentQNetwork, self).__init__() # 可以是MLP或RNN(DRQN),取决于可观察性需求 self.fc1 = nn.Linear(obs_dim, 64) self.fc2 = nn.Linear(64, 64) self.fc3 = nn.Linear(64, action_dim) # 每个动作的Q值
def forward(self, obs: torch.Tensor) -> torch.Tensor:
x = F.relu(self.fc1(obs))
x = F.relu(self.fc2(x))
q_values = self.fc3(x)
return q_values
# 简化的QMIX混合网络 class QMixer(nn.Module): def __init__(self, num_agents: int, global_state_dim: int, mixing_embed_dim: int = 32): super(QMixer, self).__init__() self.num_agents = num_agents self.state_dim = global_state_dim self.embed_dim = mixing_embed_dimW1的超网络(生成正权重)
self.hyper_w1 = nn.Sequential(
nn.Linear(self.state_dim, 64), nn.ReLU(),
nn.Linear(64, self.num_agents * self.embed_dim)
)b1的超网络
self.hyper_b1 = nn.Linear(self.state_dim, self.embed_dim)
W2的超网络(生成正权重)
self.hyper_w2 = nn.Sequential(
nn.Linear(self.state_dim, 64), nn.ReLU(),
nn.Linear(64, self.embed_dim) # 输出大小embed_dim -> 重塑为(embed_dim, 1)
)b2的超网络(标量偏置)
self.hyper_b2 = nn.Sequential(
nn.Linear(self.state_dim, 32), nn.ReLU(), nn.Linear(32, 1)
)def forward(self, agent_qs: torch.Tensor, global_state: torch.Tensor) -> torch.Tensor:
agent_qs形状:(batch_size, num_agents)
global_state形状:(batch_size, global_state_dim)
batch_size = agent_qs.size(0)
agent_qs_reshaped = agent_qs.view(batch_size, 1, self.num_agents)从全局状态生成权重/偏置
w1 = torch.abs(self.hyper_w1(global_state)).view(batch_size, self.num_agents, self.embed_dim)
b1 = self.hyper_b1(global_state).view(batch_size, 1, self.embed_dim)w2 = torch.abs(self.hyper_w2(global_state)).view(batch_size, self.embed_dim, 1)
b2 = self.hyper_b2(global_state).view(batch_size, 1, 1)混合层(确保第一层后有非线性如ELU/ReLU)
hidden = F.elu(torch.bmm(agent_qs_reshaped, w1) + b1) # (batch, 1, embed_dim)
q_tot = torch.bmm(hidden, w2) + b2 # (batch, 1, 1)
return q_tot.view(batch_size, 1) # 返回形状(batch, 1)
-
奖励表现(共享): 智能体展示了显著的学习进步。共享奖励曲线呈现明显的上升趋势,特别是在移动平均线中表现突出,从初始的显著负值增长至最终约-10至-20的水平。尽管性能有了实质性改善,但奖励仍然存在波动且未能稳定达到正值区间。
-
TD损失: 平均TD损失(注意采用对数刻度)在前约150回合内急剧下降,幅度接近两个数量级,表明Q网络和混合器架构迅速学会了对联合动作价值进行有效近似。随后损失值在一个较低水平趋于稳定,表明系统成功学习到了相对于当前策略的准确值函数表示。
-
探索行为: Epsilon参数在整个训练过程中保持稳定但缓慢的衰减趋势。这种设计确保了持续的环境探索能力,可能导致奖励指标的持续性波动,但同时允许智能体有效逃离局部最优解。
16、HAC:层次化结构解决长时域任务
-
高层(第1层): 接收当前状态 s 和最终目标 G 作为输入,其策略 (π_1) 为低层生成子目标 g₀。
-
低层(第0层): 接收当前状态 s 和来自高层的子目标 g₀,其策略 (π_0) 选择原始动作 a,旨在在固定时间范围 H 内实现子目标。低层根据子目标完成情况获得内在奖励,用于更新其策略参数。
-
高层更新机制: 高层获取低层执行过程中累积的环境奖励总和,并基于状态转换(从设置子目标的初始状态到低层执行完毕的最终状态)来优化其策略。
# 目标条件Q网络 (可用于HAC中的Actor/Critic代理) # 假设状态和目标作为输入连接在一起 class GoalConditionedQNetwork(nn.Module): def __init__(self, input_dim: int, action_dim: int): super(GoalConditionedQNetwork, self).__init__() self.fc1 = nn.Linear(input_dim, 128) self.fc2 = nn.Linear(128, 128) # 输出取决于层次: # L0: 原始动作的Q值 # L1: 选择离散子目标的Q值 self.fc3 = nn.Linear(128, action_dim)def forward(self, state_goal_concat: torch.Tensor) -> torch.Tensor:
x = F.relu(self.fc1(state_goal_concat))
x = F.relu(self.fc2(x))
q_values = self.fc3(x)
return q_values— 网络维度 —
state_dim = env.state_dim
goal_dim = env.goal_dim # 如果目标是状态,通常与state_dim相同
primitive_action_dim = env.action_dim
subgoal_action_dim = env.rows * env.cols # 如果子目标是离散网格单元
low_level_net = GoalConditionedQNetwork(state_dim + goal_dim, primitive_action_dim)
high_level_net = GoalConditionedQNetwork(state_dim + goal_dim, subgoal_action_dim)
# 简化的后见之明回放缓冲区概念 class HindsightReplayBuffer: def __init__(self, capacity: int, hindsight_prob: float = 0.8): self.memory = deque([], maxlen=capacity) self.hindsight_prob = hindsight_probdef push(self, state, action, reward, next_state, goal, done, level, achieved_goal):
存储完整的转换,包括预期目标和实际达到的目标
self.memory.append({
‘state’: state, ‘action’: action, ‘reward’: reward,
‘next_state’: next_state, ‘goal’: goal, ‘done’: done,
‘level’: level, ‘achieved_goal’: achieved_goal
})def sample(self, batch_size: int, level: int):
1. 筛选缓冲区中正确’level’的转换
2. 从这些转换中采样一批
3. 对于批次中的每个转换:
- 保留原始转换(state, action, reward, next_state, goal, done)
- 以’hindsight_prob’的概率:
- 创建一个新的后见之明转换:
- 使用相同的state, action, next_state。
- 用’achieved_goal’替换’goal’。
- 根据next_state是否匹配新的后见之明目标重新计算’reward’
(例如,如果匹配则为0,如果不匹配则为-1,用于L0内在奖励)。
- 根据是否达到后见之明目标重新计算’done’。
- 将此后见之明转换添加到正在准备的批次中。
4. 将最终批次(原始+后见之明)转换为张量。
-
奖励表现: 实验数据显示智能体表现出负向学习趋势,环境奖励在整个训练过程中持续下降。
-
执行效率: 未观察到效率提升;回合长度持续维持在接近最大允许步数的水平。
-
层次化学习问题: 高层损失函数呈现上升趋势,表明目标设定策略性能有所恶化。低层损失数据缺失或未显示,这进一步表明子目标实现层次也存在学习障碍。
-
探索策略: 尽管实施了标准线性epsilon衰减探索机制,但未能有效解决基础学习问题。
17、MCTS:基于模拟的探索规划算法
-
选择(Selection): 根据选择策略(如UCB1)递归地选择子节点,从根节点遍历现有树结构。该策略平衡了探索(访问较少探索的节点)与利用(访问过去模拟中获得高平均奖励的节点)。此过程持续直到达到一个叶节点(尚未完全扩展的节点)。
-
扩展(Expansion): 若叶节点非终止节点,通过选择一个未尝试的动作并模拟执行,生成新状态,并将表示该新状态的节点添加到搜索树中。
-
模拟(Simulation/Rollout): 从新扩展节点(若无法扩展则为选择的叶节点)开始,使用简单、高效的"rollout策略"(通常为随机动作选择)进行模拟,直到回合结束或达到预设深度限制。记录此模拟过程获得的累积奖励。
-
反向传播(Backpropagation): 使用模拟获得的结果更新选择和扩展阶段访问过的所有节点的统计数据,包括访问计数和累积奖励值。
class MCTSNode: """ 表示蒙特卡洛树搜索中的节点。 """ def __init__(self, state: Tuple[int, int], parent: Optional['MCTSNode'] = None, action: Optional[int] = None): self.state = state self.parent = parent self.action_that_led_here = action # 父节点采取的动作导致此节点self.children: Dict[int, MCTSNode] = {} # 映射动作 -> 子节点
获取可能动作的函数(取决于环境)
self.untried_actions: List[int] = self._get_possible_actions(state)
self.visit_count: int = 0
self.total_value: float = 0.0 # rollout奖励总和def _get_possible_actions(self, state):
占位符:用实际环境调用替换
网格世界的示例(假设env可访问或已传递):
if env.is_terminal(state): return
return list(range(env.get_action_space_size())) # 或env.get_valid_actions(state)def is_fully_expanded(self) -> bool:
return not self.untried_actionsdef is_terminal(self) -> bool:
占位符:用实际环境调用替换
return env.is_terminal(self.state)
def get_average_value(self) -> float:
return self.total_value / self.visit_count if self.visit_count > 0 else 0.0def select_best_child_uct(self, exploration_constant: float) -> ‘MCTSNode’:
“”" 选择具有最高UCT评分的子节点。“”"
best_score = -float(‘inf’)
best_child = None
for action, child in self.children.items():
if child.visit_count == 0:
score = float(‘inf’) # 优先选择未访问节点
else:
exploit = child.get_average_value()
explore = exploration_constant * math.sqrt(math.log(self.visit_count) / child.visit_count)
score = exploit + explore
if score > best_score:
best_score = score
best_child = child
if best_child is None: # 只应在节点还没有子节点时发生
return self # 理想情况下不应在没有子节点的节点上调用
return best_child
-
性能表现: MCTS算法持续实现正向总奖励,移动平均值稳定维持在+6至+7区间。这表明在给定的模拟预算(100次模拟)条件下,规划过程能有效找到高奖励路径。
-
执行效率: 回合长度普遍较低且相对稳定,平均约为30-40步。数据未显示明显的下降趋势,这表明MCTS从早期阶段就能够发现高效路径,而非通过多回合学习逐步提升效率。
-
规划特性: 作为规划算法,MCTS的性能主要取决于每个回合内的搜索质量。结果显示搜索过程持续有效,但不呈现传统强化学习算法中参数更新带来的典型"学习曲线"特征。
-
路径可视化: 最后一个回合的智能体轨迹展示了从起点('S')到目标('G')的清晰、有向路径,直观验证了规划成功。
18、PlaNet:潜在空间规划网络
-
"潜在状态"可由环境的状态向量(或其简单MLP编码)近似表示
-
世界模型简化为预测下一状态向量和奖励的多层感知器(MLP)网络
# 简化的动力学模型(预测下一个状态向量和奖励) class DynamicsModel(nn.Module): def __init__(self, state_dim: int, action_dim: int, hidden_dim: int = 200): super(DynamicsModel, self).__init__() self.fc1 = nn.Linear(state_dim + action_dim, hidden_dim) self.fc2 = nn.Linear(hidden_dim, hidden_dim) self.fc_next_state = nn.Linear(hidden_dim, state_dim) self.fc_reward = nn.Linear(hidden_dim, 1)def forward(self, state: torch.Tensor, action: torch.Tensor) -> Tuple[torch.Tensor, torch.Tensor]:
连接状态和动作
x = torch.cat([state, action], dim=-1)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
pred_next_state = self.fc_next_state(x)
pred_reward = self.fc_reward(x)
return pred_next_state, pred_reward
# CEM规划器概述 def cem_planner(model: DynamicsModel, initial_state: torch.Tensor, horizon: int, num_candidates: int, num_elites: int, num_iterations: int, gamma: float, action_low, action_high, action_dim, device) -> torch.Tensor:初始化动作分布(例如,高斯mean=0, std=high)
action_mean = torch.zeros(horizon, action_dim, device=device)
action_std = torch.ones(horizon, action_dim, device=device) # 开始时方差高for _ in range(num_iterations):
1. 采样候选动作序列(batch, horizon, action_dim)
action_dist = Normal(action_mean, action_std)
candidate_actions = action_dist.sample((num_candidates,))
candidate_actions = torch.clamp(candidate_actions, torch.tensor(action_low, device=device), torch.tensor(action_high, device=device))2. 使用模型评估序列
total_rewards = torch.zeros(num_candidates, device=device)
current_states = initial_state.repeat(num_candidates, 1)
with torch.no_grad():
for t in range(horizon):
actions_t = candidate_actions[:, t, :]
next_states, rewards = model(current_states, actions_t)
total_rewards += (gamma ** t) * rewards.squeeze(-1) # 确保reward被挤压
current_states = next_states3. 选择精英动作序列
_, elite_indices = torch.topk(total_rewards, num_elites)
elite_actions = candidate_actions[elite_indices]4. 重新拟合动作分布
action_mean = elite_actions.mean(dim=0)
action_std = elite_actions.std(dim=0) + 1e-6 # 添加epsilon保持稳定性返回最终平均序列的第一个动作
return action_mean[0]
# --- 模型训练概述 --- # (假设已定义model, optimizer, sequence_buffer)for _ in range(num_train_steps):
- 从sequence_buffer中采样序列批次
- 对于序列中的每一步(或其子集):
- 从批次获取state_t, action_t, reward_t, next_state_t
- 预测next_state_pred, reward_pred = model(state_t, action_t)
- 计算损失 = MSE(next_state_pred, next_state_t) + MSE(reward_pred, reward_t)
- 平均批次/步骤的损失
- optimizer.zero_grad()
- loss.backward()
optimizer.step()
-
奖励表现: PlaNet展现出显著的学习进展。每回合平均奖励从极低的初始值(约-800)快速提升至较高水平(移动平均值达到约-100至-200)。然而,即使在初始快速改善后,迭代间的表现仍存在明显波动。
-
模型学习效果: 平均模型损失(对数刻度)在初期阶段(前~25次迭代)大幅下降,降低了约两个数量级。随后损失在较低值处趋于稳定,表明PlaNet能够迅速学习钟摆系统动力学和奖励预测的准确模型。
-
基于模型的学习有效性: 奖励的显著改善与模型损失的快速下降呈现强相关性。这凸显了PlaNet的核心优势:通过快速构建准确的世界模型,使其规划组件能够发现高奖励的动作策略。
算法选择指南
本文代码:
https://github.com/FareedKhan-dev/all-rl-algorithms