清华&上海AI Lab提出GenPRM,用生成式过程奖励模型提升LLM推理能力。1.5B小模型通过测试时扩展超越GPT-4o,还能指导模型自我改进。
原文标题:过程奖励模型也可以测试时扩展?清华、上海AI Lab 23K数据让1.5B小模型逆袭GPT-4o
原文作者:机器之心
冷月清谈:
怜星夜思:
2、文章提到 GenPRM 使用了相对进步估计(RPE)来改进硬估计,那 RPE 的核心思想是什么?相比于传统的硬估计,RPE 有哪些优势和劣势?
3、GenPRM 在测试时使用了多数投票(Maj@8)的计算扩展策略,这种策略的原理是什么?为什么可以通过增加计算资源来提升评估精度?有没有其他更高效的测试时扩展策略?
原文内容
赵俭,北京邮电大学本科三年级,研究方向为大语言模型。刘润泽,清华大学硕士二年级,师从李秀教授,研究方向为大语言模型与强化学习,特别关注大模型推理能力增强与测试时间扩展,在 NeurIPS、ICML、ICLR、AAAI 等顶级学术会议发表多篇论文,个人主页:ryanliu112.github.io。
随着 OpenAI o1 和 DeepSeek R1 的爆火,大语言模型(LLM)的推理能力增强和测试时扩展(TTS)受到广泛关注。然而,在复杂推理问题中,如何精准评估模型每一步回答的质量,仍然是一个亟待解决的难题。传统的过程奖励模型(PRM)虽能验证推理步骤,但受限于标量评分机制,难以捕捉深层逻辑错误,且其判别式建模方式限制了测试时的拓展能力。
那么,是否有办法通过测试时拓展提升过程奖励模型的过程监督推理能力呢?
为此,清华大学联合上海 AI Lab 提出生成式过程奖励模型 ——GenPRM,将生成式思维链推理(CoT)与代码验证相结合,并引入测试时拓展机制,为过程监督推理提供了新思路。与 DeepSeek 近期发布的逐点生成奖励模型(GRM)类似,GenPRM 也通过生成式建模和测试时扩展增强奖励模型的推理能力,但 GenPRM 更专注于过程奖励模型,弥补了 GRM 在过程监督方面的不足。
-
论文标题:GenPRM: Scaling Test-Time Compute of Process Reward Models via Generative Reasoning
-
论文链接:http://arxiv.org/abs/2504.00891
-
项目链接:https://ryanliu112.github.io/GenPRM
-
GitHub:https://github.com/RyanLiu112/GenPRM
-
HuggingFace:https://huggingface.co/GenPRM
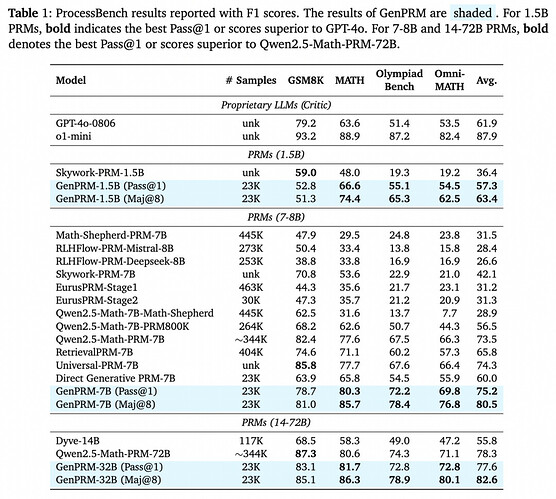
在 ProcessBench 等数学推理基准的测试中,GenPRM 展现出惊人实力:仅 1.5B 参数的模型通过测试时扩展超越 GPT-4o,而 7B 参数版本更是击败 72B 参数的 Qwen2.5-Math-PRM-72B,同时表现出强大的步骤级批评能力。
GenPRM:从评分到推理,再到测试时扩展
现有过程奖励模型依赖分类器式的标量评分,这种 “黑箱” 机制导致两个核心问题:一是无法解释错误根源,仅能判断步骤 “对错”,却无法解释 “为何错”,二是无法通过增加模型测试时间计算资源提升判断精度。
生成式过程奖励模型
为了突破这些瓶颈,GenPRM 引入生成式设计,彻底革新过程监督范式:
-
思维链推理:GenPRM 模拟人类解题时的逻辑推导,对每一步推理进行自然语言分析,提供透明、可解释的步骤评估。
-
代码验证:为确保推理的可靠性,GenPRM 还会生成并执行对应数学运算的 Python 代码,将文字推导与实际计算结果交叉验证。例如,在求解三角函数表达式时,模型先分析角度转换的合理性,再通过代码计算具体数值,避免 “符号推导正确但计算失误” 的情况。
其奖励推理过程可以表示为:
其中 s_t 为当前状态,a_t 为当前步骤,v_1:t−1 和 f_1:t-1 分别为之前步骤的推理过程和代码执行反馈,v_t 和 f_t 为当前步骤的推理与反馈。这种 “先解释、再验证” 的机制不仅能判断对错,还能提供步骤级别的批评改进建议和严谨准确的反馈,大幅提升了过程监督的深度和实用性。
测试时扩展
在推理阶段,GenPRM 通过并行采样 N 条推理路径,综合多条路径的奖励值并取平均,得到最终奖励:
这种策略充分利用额外计算资源,进一步提升评估精度,使小模型也能在复杂任务中表现出色。
数据高效:23K 样本背后的合成秘密
GenPRM 的另一个亮点是仅使用 23K 训练样本就取得了优异的性能,远少于许多模型动辄数十万级的数据量(如 PRM800K 需 80 万人工标注),其高效性源于独特的数据合成方法,结合相对进步估计(RPE)和代码验证,生成高质量的过程监督数据。
通过相对进步估计改进硬估计
传统过程奖励模型通过蒙特卡罗(MC)分数进行硬估计,研究者观察到尽管许多步骤的 MC 分数大于 0,但这些步骤是却存在错误。RPE 通过比较当前状态和上一状态的 MC 分数,用 “进步幅度” 评估每步质量,比传统硬标签更准确。其形式化如下:
其中,MC (s_t, a_t) 表示当前步骤的蒙特卡罗分数,MC (s_t) 表示上一步骤的蒙特卡罗分数。若进步幅度低于阈值(ϵ=0.8),则判定步骤无效;若首步错误(MC 为 0),后续步骤分数归零。这种方法显著提升标签准确性,避免了硬估计的误判。
代码验证驱动的数据合成
研究者利用 QwQ-32B 模型合成 CoT 和代码验证推理数据,通过在 Python 环境中真实执行代码重复检验 CoT 推理过程。使用共识过滤(过滤率 51%),保留高质量过程监督数据,最终得到 23K 训练数据集。
测试时扩展:小模型的逆袭
在 ProcessBench 过程监督基准测试中,GenPRM 展现出显著优势:
-
仅用 23K 训练数据的 1.5B GenPRM,通过多数投票(Maj@8)的测试时计算扩展策略,其 F1 分数超越 GPT-4o;
-
7B 版本的 GenPRM 以 80.5% 的 F1 分数一举超过 72B 参数的 Qwen2.5-Math-PRM-72B。
这一结果证明,测试时扩展能有效放大过程奖励模型的能力,使小模型实现性能飞跃。
此外,GenPRM 同样适用于策略模型测试时扩展。通过 Best-of-N 实验,GenPRM-7B 展现出相比于基线方法更加优异的筛选能力,并可通过测试时扩展进一步增强过程监督能力。
从验证器到批评者:过程奖励模型新范式
GenPRM 不仅能当 “裁判”,作为验证器(Verifier)筛选答案,还能当 “教练”,作为步骤级别的批评模型(Critic)指导策略模型迭代优化原始回答。实验表明,GenPRM 通过 3 轮反馈将策略模型的回答准确率从 45.7% 提升至 51.5%,性能提升达到基线方法的 3.4 倍。
这种 “生成 - 批评 - 反思” 的闭环,验证了 GenPRM 不仅可以作为验证器验证答案的准确性,还可以作为批评者,为模型完善自身输出提供逐步关键指导,为大语言模型的自我改进提供了可解释的技术路径。
研究者已开源代码、模型及 23K 训练数据集。该工作为大语言模型的可解释过程监督提供了新思路,未来可扩展至代码生成、多模态推理等领域。
© THE END
转载请联系本公众号获得授权
投稿或寻求报道:[email protected]