CVPR 2025论文提出BG-Triangle方法,融合贝塞尔三角形与高斯模型,有效解决3D高斯溅射技术重建边缘模糊问题,实现更清晰、参数效率更高的3D矢量重建。
原文标题:CVPR 2025高分论文:从照片重建3D矢量,告别模糊渲染,重建边缘更清晰
原文作者:机器之心
冷月清谈:
怜星夜思:
2、文章中提到BG-Triangle使用更少的图元数量就能实现高质量的渲染,那么在实际应用中,这对于硬件设备有什么影响?能否降低对显卡等硬件的要求?
3、BG-Triangle的核心在于“不连续感知渲染”,这个概念听起来有些抽象,大家能否用更通俗易懂的例子解释一下,它解决了3DGS的什么问题?
原文内容
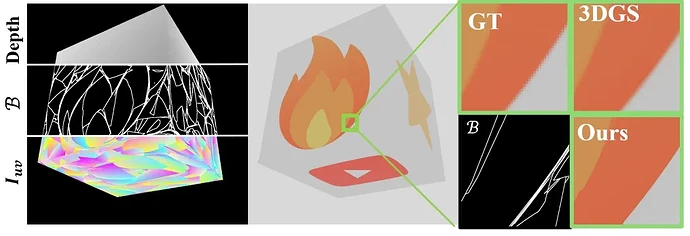
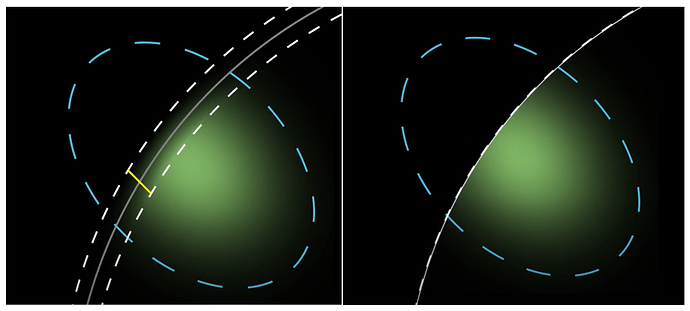
三维高斯泼溅(3D Gaussian Splatting, 3DGS)技术基于高斯分布的概率模型叠加来表征场景,但其重建结果在几何和纹理边界处往往存在模糊问题。这种模糊效应会随着重建过程中不确定性的累积而愈发显著。如图 1 所示,通过提高渲染分辨率可以明显观察到这种边界模糊现象。
图 1:BG-Triangle 的样例结果展示和对比
针对这一技术瓶颈,由比利时鲁汶大学吴旻烨与上海科技大学戴海钊等研究人员组成的团队在 CVPR 2025 上提出了创新性的解决方案 ——Bézier Gaussian Triangle(BG-Triangle)三维表征方法。该方法巧妙融合了 Bézier 三角形的矢量图形特性与高斯概率模型,不仅实现了 3D 场景的精确重建,还支持分辨率无关的可微渲染。通过引入不连续感知渲染技术,BG-Triangle 有效降低了物体边界的不确定性,从而获得更加锐利的渲染效果。与现有算法相比,该方法还具有参数量更少的显著优势。
-
论文题目:BG-Triangle: Bézier Gaussian Triangle for 3D Vectorization and Rendering
-
作者:吴旻烨、戴海钊、姚凯欣、Tinne Tuytelaars、虞晶怡
-
论文链接:https://arxiv.org/abs/2503.13961
-
项目主页和代码:https://wuminye.github.io/projects/BGTriangle/
背景介绍
在计算机图形学和 3D 计算机视觉的发展过程中,场景表示经历了从传统的离散几何表示到连续表示的演变。
早期,网格(meshes)、点云(point clouds)和体素(voxels)等传统方法被广泛应用于 3D 重建和渲染。这些方法能显式地精确建模场景,但难以实现基于图片的端到端的重建优化。
辐射场(Radiance Fields)这种 3D 表征的兴起,使得可微渲染(differentiable rendering)更加灵活,优化算法能够直接基于渲染图像的误差来更新 3D 表示。
Neural Radiance Fields (NeRF) 通过神经网络隐式编码辐射场和密度场,实现了高质量的新视角合成,但由于其连续体积表示的特性,难以精确捕捉物体的边界和几何细节。
随后,3D Gaussian Splatting (3DGS) 通过显式的高斯点云表示,提高了渲染效率和准确性,并利用连续的高斯分布实现了灵活的表征优化,适用于复杂场景的建模。
然而,这些方法在处理物体的锐利边缘时仍然存在局限性,尤其是在近距离观察时,由于渐变分布的叠加容易出现模糊或过渡不清的现象。
因此,本研究提出了一种介于离散和连续之间的三维混合表示方法,在可微渲染的框架下结合矢量图形和概率建模,利用矢量表达的灵活高效性以更少的图元数量实现更精确的几何和边界建模,为 3D 场景表示提供了一种新的解决方案。
基本原理
1. 基本元素:BG-Triangle 图元
BG-Triangle 是一种融合了贝塞尔三角形与 3D 高斯模型的场景表征方法。该方法将每个贝塞尔三角形视为一个图元,通过一组控制点参数化定义场景的局部曲面区域。作为显式几何表示,贝塞尔三角形能够清晰确定渲染视角下的图元轮廓范围。此外,通过灵活调整控制点位置,可以生成不同弯曲程度的曲面和边界。
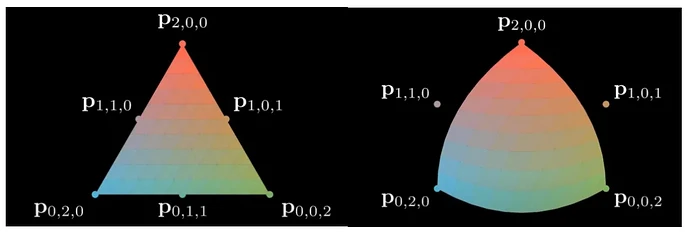
图 2:贝塞尔三角图元通过控制点来改变几何形状
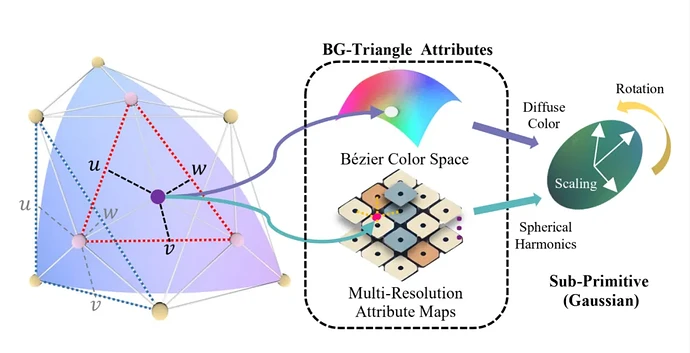
BG-Triangle 图元还编码了高斯的参数属性,包括形状、大小和颜色等信息。利用这些属性,可以在图元内自由生成用于渲染的高斯分布。这些高斯的位置与控制点相绑定,从而使图元具备可微特性。
图 3:贝塞尔三角形图元中编码的参数属性可以构造生成出任意一点的高斯分布的形状和颜色
2. 不连续感知渲染
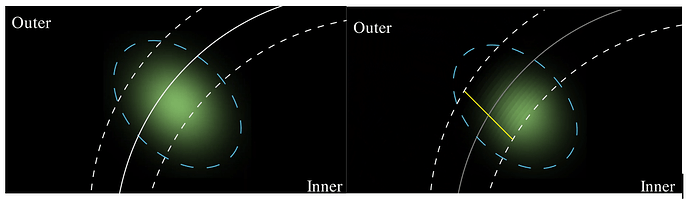
高斯虽然提供了可微的性质,但是其连续的分布无法表达不连续的纹理和几何边界。为此,研究者们使用贝塞尔三角形的渲染轮廓来对高斯的分布进行约束。具体来说,渲染算法会重新计算轮廓边界(图中的白色实线)周围区域(图中虚线之间的区域)的高斯权重,从而降低高斯分布对图元外部区域的影响效果。
图 4:BG-Triangle 使用图元的边界对高斯重新计算权重
通过调整边界宽度(即两条虚线之间的距离),可以精确控制渲染效果的锐利程度,实现不连续的边界渲染效果。
图 5:调整边界的宽度可以控制边界的锐利程度。当使用极小边界宽度时,就型成了不连续的高斯权重
3. 渲染管线与重建优化
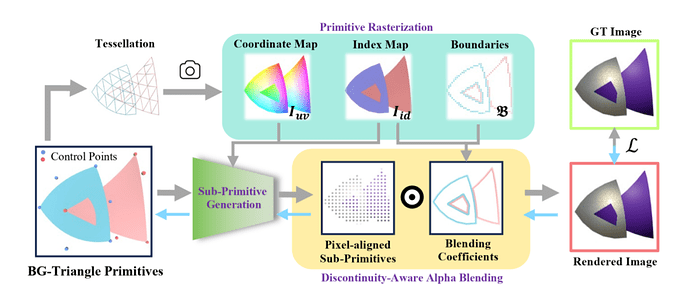
图 6:BG-Triangle 的渲染管线
BG-Triangle 的渲染管线分为两个部分。第一部分将图元渲染为目标视角下的图形缓冲区,该缓冲区包含非连续感知渲染所需的信息。这一部分可通过现有的图形光栅化管线实现。第二部分利用缓冲区信息生成像素对齐的高斯分布,并根据边界进行渲染。在此过程中,梯度通过第二部分的高斯生成模块直接传递到贝塞尔三角形图元上。具体的梯度公式推导详见原文附件,供感兴趣的读者参考。
在实现过程中,研究者首先使用粗糙的点云初始化图元位置,随后通过动态分裂和删除算法在优化过程中调整图元数量,以适应不同复杂度的场景。这种设计使得信息量较少的区域仅需少量图元即可表达,从而显著提升了信息利用效率。
图 7:组成场景的图元边界示意图。不同区域使用不同大小的图元进行自适应的表示。
实验结果
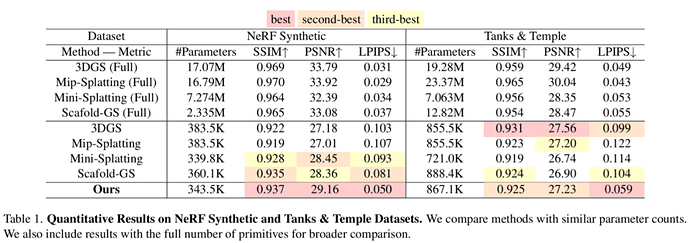
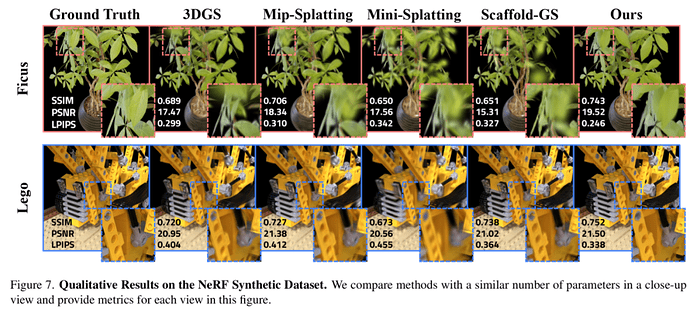
实验结果表明,BG-Triangle 在边界清晰度 和 参数效率 方面表现优越。相比 3D Gaussian Splatting(3DGS)、Mip-Splatting、Mini-Splatting 和 Scaffold-GS,能以 极少的图元数量 实现更高质量的渲染。在相似参数规模下,BG-Triangle 在 LPIPS 评分(感知质量)上显著优于其他方法,且在放大渲染中仍可保持清晰的物体边界,而 3DGS 及相关方法在近距离观察时会产生模糊或伪影。
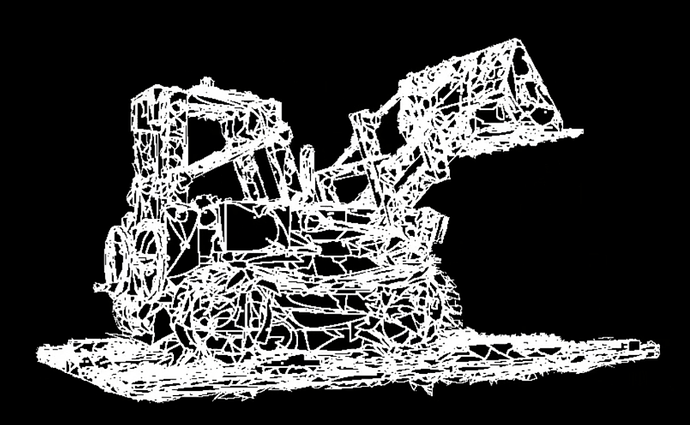
同时,通过对贝塞尔三角形矢量线段的提取,可以组成三维的线条,用于描述场景的几何特征,如图所示:
研究者们在 CUDA 中高效地实现了本文的算法,达成了实时渲染的效果。并且在 NVIDIA 3090GPU 单卡上可以半小时左右完成场景的重建。
结论
这篇研究创新性地提出了一种基于贝塞尔三角形矢量曲面的三维场景表征方法,并提供了一种有效的端到端的可微渲染和训练框架。
在渲染质量上,BG-Triangle 能够保留锐利的边界,比 3DGS 具有更好的几何精度。同时,BG-Triangle 使用更少的图元,在参数效率和渲染清晰度之间达到了更好的平衡。
BG-Triangle 在较小的参数量下有渲染质量优势,尤其是在感知质量(LPIPS 评价)上优势显著。
© THE END
转载请联系本公众号获得授权
投稿或寻求报道:liyazhou@jiqizhixin.com