深入解析Graph Transformer:一种结合图神经网络和Transformer优势,高效处理图结构数据的模型,并附带图书推荐系统代码示例。
原文标题:深入解析图神经网络:Graph Transformer的算法基础与工程实践
原文作者:数据派THU
冷月清谈:
Graph Transformer 的核心技术组件包括:
1. **图数据表示:** 使用节点和边的特征向量来表示图结构数据。节点特征可以是用户的属性、分子的特性等,边特征可以是社交关系类型、化学键类型等。
2. **自注意力机制:** 通过计算输入的加权组合来分析节点间的关联性,并通过 SoftMax 函数对注意力权重进行归一化,最终实现节点间的信息聚合。
3. **拉普拉斯位置编码:** 利用图拉普拉斯矩阵的特征向量来表示节点位置,有效捕获图的结构特征。
4. **消息传递与聚合机制:** 节点与邻接节点之间进行信息交换,并通过聚合操作将信息整合为有效的特征表示。
5. **非线性激活前馈网络:** 引入非线性特性并增强模型的模式识别能力。
6. **层归一化:** 优化训练过程和保证学习效果。
7. **局部和全局上下文:** 局部上下文关注节点的直接邻域信息,而全局上下文则捕获来自整个图结构的信息。
文章最后通过一个图书推荐系统的示例,详细介绍了 Graph Transformer 的实践过程,包括数据准备、模型构建、训练和评估等步骤,并提供了使用 PyTorch Geometric 框架的代码实现。
怜星夜思:
2、文章中提到了拉普拉斯位置编码,想了解一下除了这种方法之外,还有哪些位置编码方式可以应用于Graph Transformer?它们各自的优缺点是什么?
3、文章最后给出了一个图书推荐系统的示例,如果我想将其应用于其他类型的图数据,例如社交网络或分子图,需要进行哪些修改?
原文内容
来源:DeepHub IMBA本文约4000字,建议阅读8分钟
本文为你介绍一种将Transformer架构应用于图结构数据的特殊神经网络模型。
Graph Transformer是一种将Transformer架构应用于图结构数据的特殊神经网络模型。该模型通过融合图神经网络(GNNs)的基本原理与Transformer的自注意力机制,实现了对图中节点间关系信息的处理与长程依赖关系的有效捕获。
Graph Transformer的技术优势
在处理图结构数据任务时,Graph Transformer相比传统Transformer具有显著优势。其原生集成的图特定特征处理能力、拓扑信息保持机制以及在图相关任务上的扩展性和性能表现,都使其成为更优的技术选择。虽然传统Transformer模型具有广泛的应用场景,但在处理图数据时往往需要进行大量架构调整才能达到相似的效果。
核心技术组件
图数据表示方法
图输入数据通过节点、边及其对应特征进行表示,这些特征随后被转换为嵌入向量作为模型输入。具体包括:
-
节点特征表示
-
社交网络:用户的人口统计学特征、兴趣偏好、活动频率等量化指标
-
分子图:原子的基本特性,包括原子序数、原子质量、价电子数等物理量
-
定义:节点特征是对图中各个节点属性的数学表示,用于捕获节点的本质特性
-
边特征表示
-
社交网络:社交关系类型(如好友关系、关注关系、工作关系等)
-
分子图:化学键类型(单键、双键、三键)、键长等化学特性
-
定义:边特征描述了图中相连节点间的关系属性,为图结构提供上下文信息
技术要点:节点特征与边特征构成了Graph Transformer的基础数据表示,这种表示方法从根本上改变了关系型数据的建模范式。
自注意力机制的技术实现
自注意力机制通过计算输入的加权组合来实现节点间的关联性分析。在图结构环境下,该机制具有以下关键技术要素:
数学表示
-
节点特征向量:每个节点i对应一个d维特征向量h_i
-
边特征向量:边特征e_ij表征连接节点i和j之间的关系属性
注意力计算过程
注意力分数计算注意力分数评估节点间的相关性强度,综合考虑节点特征和边属性,计算公式如下:
![]()
其中:
-
W_q, W_k, W_e:分别为查询向量、键向量和边特征的可训练权重矩阵
-
a:可训练的注意力向量
-
∥:向量拼接运算符
注意力权重归一化原始注意力分数通过SoftMax函数在节点的邻域内进行归一化处理:
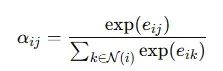
N(i)表示节点i的邻接节点集合。
信息聚合机制每个节点通过加权聚合来自邻域节点的信息:

W_v表示值投影的可训练权重矩阵。
Graph Transformer中自注意力机制的技术优势
自注意力机制在Graph Transformer中的应用实现了节点间的动态信息交互,显著提升了模型对图结构数据的处理能力。
拉普拉斯位置编码技术
拉普拉斯位置编码利用图拉普拉斯矩阵的特征向量来实现节点位置的数学表示。这种编码方法可以有效捕获图的结构特征,实现连通性和空间关系的编码。通过这种技术Graph Transformer能够基于节点的结构特性进行区分,从而在非结构化或不规则图数据上实现高效学习。
消息传递与聚合机制
消息传递和聚合机制是图神经网络的核心技术组件,在Graph Transformer中具有重要应用:
-
消息传递实现节点与邻接节点间的信息交换
-
聚合操作将获取的信息整合为有效的特征表示
这两个技术组件的协同作用使图神经网络,特别是Graph Transformer能够学习到节点、边和整体图结构的深层表示,为复杂图任务的求解提供了技术基础。
非线性激活前馈网络
前馈网络结合非线性激活函数在Graph Transformer中扮演着关键角色,主要用于优化节点嵌入、引入非线性特性并增强模型的模式识别能力。
网络结构设计

核心组件包括:
-
h_i:节点的输入嵌入向量
-
W_1, W_2:线性变换层的权重矩阵
-
b_1, b_2:偏置向量
-
激活函数:支持多种非线性函数(LeakyReLU、ReLU、GELU、tanh等)
-
Dropout机制:可选的正则化技术,用于防止过拟合
非线性激活的技术必要性
非线性激活函数的引入具有以下关键作用:
-
实现复杂函数的逼近能力
-
防止网络退化为简单的线性变换
-
使模型能够学习图数据中的层次化非线性关系
层归一化技术实现
层归一化是Graph Transformer中用于优化训练过程和保证学习效果的核心技术组件。该技术通过对层输入进行标准化处理,显著改善了训练动态特性和收敛性能,尤其在深层网络架构中表现突出。
层归一化的应用位置
在Graph Transformer架构中,层归一化主要在以下三个关键位置实施:
自注意力机制后端
-
对注意力机制生成的节点嵌入进行归一化处理
-
确保特征分布的稳定性
前馈网络输出端
-
标准化前馈网络中非线性变换的输出
-
控制特征尺度
残差连接之间
-
缓解多层堆叠导致的梯度不稳定问题
-
优化深层网络的训练过程
局部上下文与全局上下文技术
局部上下文聚焦于节点的直接邻域信息,包括相邻节点及其连接边。
应用示例
-
社交网络:用户的直接社交关系网络
-
分子图:中心原子与直接成键原子的局部化学环境
技术重要性
邻域信息处理
-
捕获节点与邻接节点的交互模式
-
提供局部结构特征
精细特征提取
-
获取用于链接预测的局部拓扑特征
-
支持节点分类等精细化任务
实现方法
消息传递机制
-
采用GCN、GAT等算法进行邻域信息聚合
-
实现局部特征的有效提取
注意力权重分配
-
基于重要性评估为邻接节点分配权重
-
优化局部信息的利用效率
技术优势
-
提供精确的局部结构表示
-
实现计算资源的高效利用
全局上下文技术实现
全局上下文技术旨在捕获和处理来自整个图结构或其主要部分的信息。
整体特征捕获
-
识别图结构中的宏观模式
-
分析全局关系网络
结构特征编码
-
量化中心性指标
-
评估整体连通性
实现方法
位置编码技术
-
使用拉普拉斯特征向量
-
实现Graphormer位置编码
全局注意力机制
-
实现全图范围的信息聚合
-
支持长程依赖关系建模
技术优势
深度上下文理解
-
超越局部邻域的信息获取
-
捕获复杂的结构依赖关系
增强表示能力
-
优化图级任务性能
-
提升分类回归准确度
损失函数设计
多层次任务支持
节点级任务
-
分类任务:采用交叉熵损失
-
回归任务:采用均方误差损失
边级任务
-
实现二元交叉熵损失
-
支持排序损失函数
图级任务
-
基于节点级损失函数扩展
-
适用于全局嵌入评估
Graph Transformer的工程实现
本节将通过一个完整的图书推荐系统示例,详细介绍Graph Transformer的实践实现过程。我们使用PyTorch Geometric框架构建模型,该框架提供了丰富的图神经网络工具集。
import torch import torch.nn as nn import torch.nn.functional as F from torch_geometric.nn import MessagePassing, GATConv, global_mean_pool from torch_geometric.data import Data, DataLoader from sklearn.model_selection import train_test_split import os构建异构图数据结构
该函数创建一个包含图书节点和类型节点的异构图示例
def create_sample_graph():
定义图书节点特征矩阵 (3个图书节点,每个具有5维特征)
book_features = torch.tensor([
[0.8, 0.2, 0.5, 0.3, 0.1], # 第一本图书的特征向量
[0.1, 0.9, 0.7, 0.4, 0.3], # 第二本图书的特征向量
[0.6, 0.1, 0.8, 0.7, 0.5] # 第三本图书的特征向量
], dtype=torch.float)定义类型节点特征矩阵 (2个类型节点,每个具有3维特征)
genre_features = torch.tensor([
[1.0, 0.2, 0.3], # 第一个类型的特征向量
[0.7, 0.6, 0.8] # 第二个类型的特征向量
], dtype=torch.float)合并所有节点的特征矩阵
x = torch.cat([book_features, genre_features], dim=0)
定义图的边连接关系
edge_index中每一列表示一条边,[源节点,目标节点]
edge_index = torch.tensor([
[0, 1, 2, 0, 1], # 源节点索引
[3, 4, 3, 4, 3] # 目标节点索引
], dtype=torch.long)定义边特征 (每条边的权重)
edge_attr = torch.tensor([
[0.9], [0.8], [0.7], [0.6], [0.5]
], dtype=torch.float)定义节点标签 (用于推荐任务的二元分类)
y = torch.tensor([0, 1, 0, 0, 0], dtype=torch.long)
return Data(x=x, edge_index=edge_index, edge_attr=edge_attr, y=y)
实现消息传递层
该层负责节点间的信息交换和特征转换
class MessagePassingLayer(MessagePassing):
def init(self, in_channels, out_channels):
super(MessagePassingLayer, self).init(aggr=‘mean’) # 使用平均值作为聚合函数
self.lin = nn.Linear(in_channels, out_channels) # 线性变换层def forward(self, x, edge_index):
return self.propagate(edge_index, x=self.lin(x))def message(self, x_j):
return x_j # 直接传递相邻节点的特征def update(self, aggr_out):
return aggr_out # 返回聚合后的特征Graph Transformer模型定义
class GraphTransformer(nn.Module):
def init(self, input_dim, hidden_dim, output_dim):
super(GraphTransformer, self).init()模型组件初始化
self.message_passing = MessagePassingLayer(input_dim, hidden_dim) # 消息传递层
self.gat = GATConv(hidden_dim, hidden_dim, heads=4, concat=False) # 图注意力层前馈神经网络
self.ffn = nn.Sequential(
nn.Linear(hidden_dim, hidden_dim),
nn.ReLU(),
nn.Linear(hidden_dim, output_dim)
)层归一化
self.norm1 = nn.LayerNorm(hidden_dim)
self.norm2 = nn.LayerNorm(output_dim)def forward(self, data):
x, edge_index, edge_attr = data.x, data.edge_index, data.edge_attr第一阶段:消息传递
x = self.message_passing(x, edge_index)
x = self.norm1(x)第二阶段:注意力机制
x = self.gat(x, edge_index)
x = self.norm2(x)第三阶段:特征转换
out = self.ffn(x)
return out定义交叉熵损失函数用于分类任务
criterion = nn.CrossEntropyLoss()
模型训练函数
def train_model(model, loader, optimizer, regularization_lambda):
model.train()
total_loss = 0
for data in loader:
optimizer.zero_grad() # 清空梯度
out = model(data) # 前向传播
loss = criterion(out, data.y) # 计算损失添加L2正则化以防止过拟合
l2_reg = sum(param.pow(2.0).sum() for param in model.parameters())
loss += regularization_lambda * l2_regloss.backward() # 反向传播
optimizer.step() # 参数更新
total_loss += loss.item()
return total_loss / len(loader)模型评估函数
def test_model(model, loader):
model.eval()
correct = 0
total = 0
with torch.no_grad(): # 禁用梯度计算
for data in loader:
out = model(data)
pred = out.argmax(dim=1) # 获取预测结果
correct += (pred == data.y).sum().item()
total += data.y.size(0)
return correct / total模型保存函数
def save_model(model, path=“best_model.pth”):
torch.save(model.state_dict(), path)模型加载函数
def load_model(model, path=“best_model.pth”):
model.load_state_dict(torch.load(path))
return model主程序入口
if name == “main”:
数据准备
graph_data = create_sample_graph()
train_data, test_data = train_test_split([graph_data], test_size=0.2)
train_loader = DataLoader(train_data, batch_size=1, shuffle=True)
test_loader = DataLoader(test_data, batch_size=1, shuffle=False)模型初始化
input_dim = graph_data.x.size(1) # 输入特征维度
hidden_dim = 16 # 隐藏层维度
output_dim = 2 # 输出维度(二分类)
model = GraphTransformer(input_dim, hidden_dim, output_dim)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)训练循环
best_accuracy = 0
for epoch in range(20):训练和评估
train_loss = train_model(model, train_loader, optimizer, regularization_lambda=1e-4)
accuracy = test_model(model, test_loader)
print(f"Epoch {epoch + 1}, Loss: {train_loss:.4f}, Accuracy: {accuracy:.4f}")保存最佳模型
if accuracy > best_accuracy:
best_accuracy = accuracy
save_model(model)加载最佳模型用于预测
model = load_model(model)
生成图书推荐
model.eval()
book_embeddings = model(graph_data)
print(“Generated book embeddings for recommendation:”, book_embeddings)
本实现展示了Graph Transformer在图书推荐系统中的应用,涵盖了数据结构设计、模型构建、训练过程和推理应用的完整流程。通过合理的架构设计和优化策略,该实现能够有效处理图书与类型之间的复杂关系,为推荐系统提供可靠的特征表示。
总结
Graph Transformer作为图神经网络领域的重要创新,通过将Transformer的自注意力机制与图结构数据处理相结合,为复杂网络数据的分析提供了强大的技术方案。作为图神经网络技术在现代人工智能领域的重要分支,Graph Transformer展现了其在处理复杂网络数据方面的独特优势。无论是在算法设计还是工程实现上,它都为解决实际问题提供了新的思路和方法。通过本文的系统讲解,读者不仅能够理解Graph Transformer的工作原理,更能够掌握将其应用于实际问题的技术能力。
本文不仅是对Graph Transformer技术的深入解析,更是一份从理论到实践的完整技术指南,为那些希望在图神经网络领域深入发展的技术人员提供了宝贵的学习资源。






