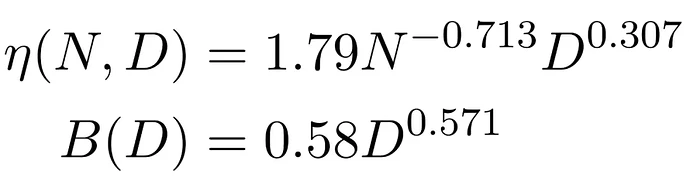阶跃星辰开源LLM超参数优化工具，揭示最优学习率和批量大小的缩放规律，适用于不同模型和数据分布，为大模型预训练提供实用指导。
原文标题：百万美金炼出「调参秘籍」！阶跃星辰开源LLM最优超参工具
原文作者：机器之心
冷月清谈：
阶跃星辰研究团队通过大规模实验，耗费近百万美元的GPU资源，训练了3700个不同规模的LLM，揭示了LLM超参数优化的普适性缩放规律（Step Law）。该规律表明，最优学习率随模型和数据规模呈幂律变化，而最优批量大小主要与数据规模相关。研究发现，超参数优化的Landscape呈现凸性特征，存在稳定且易寻的最优区域。团队开源了最优超参数估算工具，并公开了loss热力图。Step Law在不同模型形状、架构和数据分布上表现出稳定性，并对学习率调度策略进行了优化，强调固定最小学习率的重要性。研究团队还开源了拟合方法，为大模型预训练提供了开箱即用的工具，并计划进一步研究超大模型性能预测等问题。
怜星夜思：
1、文章中提到Step Law在不同数据分布下都表现出了稳定性，那么在实际应用中，如果我们混合了多种不同领域的数据进行训练，例如同时包含文本、图像和音频数据，这个规律还适用吗？
2、文章提到Step Law在MoE模型上也表现出良好的泛化性，那么对于更大规模的MoE模型，比如专家数量非常多，或者专家容量很小的情况下，这个规律还适用吗？
3、文章中提到了学习率调度策略的优化，固定最小学习率比传统衰减策略更好。那么，除了这两种策略，还有没有其他更有效的学习率调度策略？例如，最近比较火的自适应学习率调整方法，它们与Step Law是否兼容？
2、文章提到Step Law在MoE模型上也表现出良好的泛化性，那么对于更大规模的MoE模型，比如专家数量非常多，或者专家容量很小的情况下，这个规律还适用吗？
3、文章中提到了学习率调度策略的优化，固定最小学习率比传统衰减策略更好。那么，除了这两种策略，还有没有其他更有效的学习率调度策略？例如，最近比较火的自适应学习率调整方法，它们与Step Law是否兼容？
原文内容
机器之心发布
机器之心编辑部
近日，阶跃星辰研究团队通过大规模实证探索，耗费了近 100 万 NVIDIA H800 GPU 小时（约百万美元），从头训练了 3,700 个不同规模，共计训了 100 万亿个 token，揭示了 LLM 超参数优化的全新的普适性缩放规律，为更好地提升 LLM 性能，提供了开箱即用的工具。该研究也是第一个全面研究模型最优超参随着 Model Shape、Dense/MoE、预训练数据分布的变化，是否稳定不变的工作。研究中凸显出 Step Law 的鲁棒性，大大增加了该工具的实用性和普适性。同时该团队正在逐步开源相关资料，包括模型、训练日志等，期待更多相关领域的人基于海量的实验结果作出更加深入的研究与解释。
-
论文标题：Predictable Scale: Part Ⅰ — Optimal Hyperparameter Scaling Law in Large Language Model Pretraining
-
论文链接：https://arxiv.org/abs/2503.04715
-
工具链接：https://step-law.github.io/
-
开源地址：https://github.com/step-law/steplaw
-
训练过程：https://wandb.ai/billzid/predictable-scale
海量实验，实证为王
研究团队从头训练了 3,700 个不同规模、不同超参数组合、不同形状、不同数据配比、不同稀疏度 (含 MoE、Dense) 的大语言模型（LLM），共训练了超 100 万亿个 token，对超参数进行了全面的网格搜索，研究团队发现了一条普适的缩放法则 (简称 Step Law)：最优学习率随模型参数规模与数据规模呈幂律变化，而最优批量大小主要与数据规模相关。
图一：在 400M 的 Dense LLM 上训练 40B Token（左）和在 1B 的 Dense LLM 上训练 100B Token（右）的超参 - 损失等高线图，并且对业内不同方法进行比较，所有方法都转换成了预测 Optimal Token Wise BatchSize。这里所有的等高线都是从头训练的小模型所得的真实收敛后的 Train Smooth Loss。左右两张图的所有等高线，分别来自于两组共 240 个采用不同超参（Grid Search）的端到端训练的小模型。Global Mimimum 是来 120 个小模型中最终 Train Smooth Loss 最小的那个。等高线表示距离 Global Mimimum 的从最终 loss 角度的相对距离。而超越 + 2% 的点位，并没有体现在图中。
值得关注的是，实验表明，在固定模型大小与数据规模时，超参数优化的 Landscape 呈现出明显的凸性特征，这意味着存在一个稳定且易寻的最优超参数区域。
图二：Learning Rate 与 Batch Size 在 1B 模型训练 100BToken 上的损失分布：散点图（左）与 3D 曲面（右）图中的每一个实心点都是真实值，是 120 个从头训练的一个小模型，在训练结束之后的收敛 Loss。为了展示这样的凸性，研究员们构造了如右图一样的 3 维空间，空间的横轴为 Learning Rate，纵轴为 Batch-size，高度轴为 Loss。对于这个三维空间我们进行横面和竖面的切割，如左上图得到固定不同的 Learning Rate 情况下，最终收敛的 Train Smoothed Loss 随着 Batchsize 的变化。而左下图是固定不同的 Batchsize 情况下，最终收敛的 Train Smoothed Loss 随着 Learning Rate 的变化。可以显著的观测到一种凸性，且在凸性的底端，是一个相对平坦的区域。这意味着 Optimal Learning Rate 和 Batchsize 很可能是一个比较大区域。
为了便于学界和业界应用，团队推出了一款通用的最优超参数估算工具（https://step-law.github.io），其预测结果与穷举搜索的全局最优超参数相比，性能仅有 0.09% 的差距。同时，研究团队还在该网站上公开了所有超参数组合的 loss 热力图，以进一步推动相关研究。
图三：1B 模型、100BToken 训练上的 LR 与 BS 热力图。每一个点上的数字都是从头训练的一个小模型（共训练了 120 个小模型），在训练结束之后的收敛真实 Train Smoothed Loss。红点是上述公式的预估值所对应的 BS、LR 位置。其中空白的部分，是因为种种原因训练失败的点位。所有热力图见https://step-law.github.io/
研究亮点：Step Law 的普适性，从三个不同角度
相较于现有的大模型最优超参数估算公式，团队的研究进行了极其充分的、覆盖模型参数规模（N）、训练数据规模（D）、批量大小（BS）和学习率（LR）的网格搜索，最终得到的 Step Law 则展现出显著的优越性，在适用性和准确度方面均有大幅提升。
表一：不同方法的最佳超参数缩放定律比较，其中 Data Recipe 是指是否有在不同的预训练语料的配比下的最优超参进行研究。Model Sparsity 是指是否同时支持 MoE Model 和 Dense Model，以及不同的稀疏度下的 MoE 模型。LR 指的是 learning Schedule 中的峰值 Learning Rate，其中 BS 值得是 Token Wise 的 Batch Size。
角度一：跨模型形状 (Model Shape) 的稳定性
研究还深入探讨了不同模型形状（如宽度与深度的不同组合）对缩放规律的影响，发现无论模型是以宽度为主还是深度为主，抑或是宽深平衡的设计，Step Law 均表现出了高度的稳定性。这表明，缩放规律不仅适用于特定类型的模型结构，在更广泛的架构设计空间中依然适用，为复杂模型架构的设计和优化提供了指导意义。
图四：最优超参在不同 Model Shape 下的拓扑不变性。这里的是固定了模型的非词表参数量的大小，且固定了模型的训练 Token 数，但研究团队使用了不同的 Model Shape。例如变换了层数，从左到右分别是 14/10/8 层；变换了 Model Hidden Dimension，分别包括 1280/1536/2048 这三种；同时变换了 6 种不同的 FFN 倍数 (FFN_media_dim/model_dim)，从 1.1 倍到～6.25 倍。其中红色五角星的点是 Step Law 预测的点位，可以观察到 Step_law 在 6 个不同的 Shape 上都预测到了 Global Minimum 附近。然而也可以同时观察到，不同的 Model Shape，Bottom 的一片区域的位置是会发生 shift 的。
角度二：跨模型架构的泛化性
研究结果发现，这一缩放规律不仅适用于 Dense 模型，还能很好地推广到不同稀疏度的 MoE 模型（Mixture-of-Experts），展示了极强的泛化能力。
图五：不同稀疏比下 MoE 模型的超参 - 损失等高线图。左：低稀疏度（N_a/N=0.27），中间：中等稀疏度（N_a/N=0.58，D/N=10），右：中等稀疏度、较少训练 Token 数（N_a/N=0.58，D/N=4）。研究员们在不同稀疏度，不同 D/N 的 MoE 模型配置，每一种配置都从头训练了 45 个小模型，来做最优超参搜取。共计从头训练了 495 个不同稀疏度、不同超参、不同 D/N 的 MoE 模型。从而得到了不同配置下的基于真实值的 Global Minimum Train Smoothed Loss。其中除了一组 D/N=1 的实验，其余实验 Step Law 预测位置都在 Global Minimum+0.5% 的范围之内。并且大多数配置下都在 Global Minimum+0.25% 的范围之内。充分的验证了 Step Law 的鲁棒性。详细结果可以参考论文的附录部分。
角度三：跨数据分布的稳定性
那么 Step Law 是否能兼容不同的预训练数据分布呢？研究团队进一步验证了不同数据分布下的规律一致性：无论是英语主导、中英双语、Code 和英语混合，还是代码主导的数据分布，Step Law 都表现出了稳定的性能。这为多语言、多任务场景下的实际应用提供了可靠支持。
表二：实验的不同数据分布。其中 Baseline 是得出 Step Law 的训练 Recipe。而 Code-Math，是压缩英文 web-data 的配比近一半，扩大 code-math 的比例至近 40%。而 More Code-Math 比例更加极端，将英文 web-data 的配比压缩为之前的 1/4，将 Code-math 扩大为近 2/3。EN-CN 是下调英文 web-data 的配比近一半，将余量的部分都转化为中文网页数据。
图六：不同数据分布下的超参 - 损失等高线。左：双语数据（表格中 En-CN），中间：加入 Code 数据（表格中的 Code+Math），右：主要为 Code 数据（表格中的 More Code+Math）。每一个图都是从头训练了 45 个模型，每一个模型除了 Bs/lr 不同以外，其他设置完全相同。总共训练了 135 个在三种数据分布下的模型。其中 Global Minimum 是通过这种 grid search 的方法得到的最低 Final Train Smoothed Loss 的真实值。Step Law 预测出来的最优 Batch Size/Learning Rate 都在最低 Loss +0.125%/0.25% 的范围内。
研究细节解读
1. 学习率调度策略优化
图七：不同学习率策略的比较。蓝色等高线 (传统衰减策略): 学习率会从一个最大值 (max_lr) 逐渐减小到一个最小值 (min_lr，常是峰值的十分之一)。红色等高线 (固定最终学习率策略): 保持一个固定的最小学习率 (min_lr = 1e-5)，而不是像传统方法那样与最大学习率挂钩。两张图都分别为 120 个从头训练的模型，在相同的 batch size/learning rate 范围内做的 Grid Search。红色和蓝线的 Global Minimum 都是各自配置下的真值 - 最小的 Final Train Smoothed Loss。可以观察到改成 max_lr/10 之后，蓝点会向左上方偏移，即更小的 Learning Rate 和更大的 Batchsize。如果不是对比相对值，而是对比真值，min_lr=1e-5 的最终收敛 loss 普遍小于 max_lr/10。相关的真值将陆续开源。相关的真值开源在https://github.com/step-law/steplaw
研究团队通过对比分析发现，学习率调度策略对最优超参选择产生显著影响。研究揭示了传统学习率衰减与固定最小学习率方案间的重要差异：
传统学习率衰减方案将最小学习率设为最大值的十分之一 (max_lr/10)，而团队提出的固定方案则采用恒定的绝对最小值 (1e-5)。等高线图分析清晰表明，传统衰减方法使得最优学习率区域出现明显的左偏分布 —— 即损失最小区域向较低学习率区间显著偏移。
团队通过分析了传统学习率（min_lr=max_lr/10）调度方案的局限性：采用较高初始峰值学习率时，其退火机制会同步抬升最低学习率阈值。这种耦合设计在训练末期会使学习率超出理想区间，过大的参数更新幅度引发损失函数在收敛阶段持续振荡。相比之下，固定最小学习率策略通过解耦初始学习率与终值学习率的关联，在训练后期始终维持符合梯度下降动态特性的更新步长。
此外，这种固定最终较小最终学习率的策略也与业界的训练经验相匹配，更有实际应用价值。
2. 训练损失与验证损失的最优超参一致性
图八：平滑训练损失（Final Train Smoothed Loss）的超参 - 损失等高线图（左）和验证损失（Validation Loss of Final Checkpoint）的超参 - 损失等高线图（右）。两张图都是在同一组实验下进行，对于相同的模型尺寸，相同的训练 Token 数，分别采用了 64 组不同的超参进行 Grid Search。从而得到 64 个模型的 Final Train Smoothed Loss、和 Validation Loss。
在 429M 模型上训练 40B 的 Token 进行验证，当平滑训练损失达到最优时，学习率为 1.95×10^-3，批量大小为 393,216，这一点与验证损失最优时的超参数完全重合。此外，学习率和批量大小的变化趋势在平滑训练损失和验证损失中表现出高度一致性。这一发现表明，平滑的训练损失曲线可以为实际超参数选择提供可靠的指导。尽管采用 Train Smoothed Loss 可以降低实验成本（节省了 Final Checkpoint 在 Validation Set 上推理的算力），但仍然具有一定的局限性，例如训练数据不能重复。研究团队将会陆续开源这近 4000 个模型的 Final Checkpoint，供广大研究员进行进一步的分析。
最优超参的 Scaling Law 拟合
图九：(a) 散点图表示模型规模为 N 时，经验最优学习率与批量大小的关系；(b) 散点图表示数据集规模为 D 时，经验最优学习率与批量大小的关系。曲线表示超参数缩放定律的预测结果，阴影区域表示基于采样拟合策略得到参数不确定性范围。图上的每一个点，背后都代表着 45~120 个采用了不同的超参的从头训练的模型。图上的每一个点位都在不同的 Model Size、Data Size 下通过 Grid Search 得到的最优的超参 (Optimal Learning Rate，Optimal Batch Size)。这张图总共涉及了 1912 个从头训练的 LLM。拟合方法开源在https://github.com/step-law/steplaw
通过从头训练了 1912 个 LLM，研究团队分析发现：
-
最优学习率：随模型规模增大而减小，随数据规模增大而增大。
-
最优批量大小：随数据规模增大而增大，与模型规模弱相关。
研究通过对数变换将幂律关系转化为线性形式，采用最小二乘法拟合参数，并通过 Bootstrap 采样方法提升稳健性。最终，团队提出了一套精确的预测公式，为大模型预训练的超参数设置提供了一个开箱即用的工具。据了解，在阶跃星辰真正的研发过程中，他们已经广泛使用了 Step Law，主要是在大于 1B 的模型和非极端的 D/N 下适用。
讨论与未来工作
研究团队坦言，尽管付出了很多的算力，和大量的精力来分析相关的实验。但是很多子 Topic 分析仍然是值得深究的。研究团队认为他们的这份工作仅仅是一个开始，他们会陆续将实验的各个细节整理并且开源出来，供整个社区的研究人员进行进一步分析和深入的理论解释。这些子 Topic 包括以下话题：
-
在给定模型、训练 Token 数的情况下，(Loss,bs,lr) 这三维空间是否是真正的凸性。
-
是否有更好的 optimal BS LR 的拟合方法，并且可以兼容 BS、LR 的内在关系。
-
尽管 Step Law 在不同 Model Shape、不同稀疏的 MoE 模型是鲁棒的，但是次优的区域是在不同配置下是变化的，有无更好的解释方法。
-
上文中这些基于海量 Grid Search 的数据驱动的结论的理论解释。
-
不同的超参、不同 Model Size、Model Shape、Model Sparsity 下的 Training Dynamic 研究。
为此研究团队公开了他们的开源计划，以及 Predictable Scale 系列工作的发布节奏。据了解，Predictable Scale 系列后续可能进一步讨论超大模型性能预测、Code&Math Scaling 性质、不同 Attention 类型的 Scaling 性质等问题。非常值得期待。
© THE END
转载请联系本公众号获得授权
投稿或寻求报道：[email protected]